题目内容
解答题
已知椭圆
＋
＝1的焦点为F1和F2，抛物线与椭圆在第一象限内的交点为Q，且∠F1QF2＝
，求抛物线的方程．
答案：
解析：
解析：
|
设Q(x，y)，由焦半径公式有|F1Q|＝a＋ex＝2＋ 由余弦定理得4c2＝|F1Q|2＋|F2Q|2－2·|F1Q|·|F2Q|· ∴x＝ |
x，|F2Q|＝a－ex＝2－
x．
，即12＝2(4＋
x2)－(4－
，∴y＝
．若设抛物线方程为y2＝2px(p＞0)，把点(
，
)代入可得p＝
，若设抛物线方程为x2＝2py(p＞0)，把点(
，
)代入可得p＝
．故抛物线方程为y2＝
x或x2＝
y．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
＋
＝1上一点P，到其左、右两焦点距离之比为1∶3，求点P到两准线的距离及点P的坐标．
(0，－1)和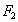
(0，1)，直线y＝4是该椭圆的一条准线．
＝1，求tan∠
＋
＝1的焦点为F1、F2，能否在x轴下方的椭圆弧上找到一点M，使M到下准线的距离|MN|等于点M到焦点F1、F2的距离的比例中项？若存在，求出M点坐标；若不存在，说明理由．
＋
＝1(a＞b＞0)上有两点A、B，直线y＝x＋m上有两点C、D，且ABCD是正方形，正方形的外接圆的方程为x2＋y2－2y－8＝0，求椭圆和直线的方程．