题目内容
4.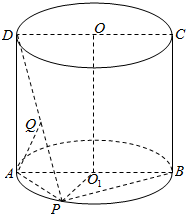 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.(Ⅰ)求证:AQ⊥PB;
(Ⅱ)若线段PD的长为$2\sqrt{3}$,求圆柱OO1的体积.
分析 (1)由圆柱得到结构特征可知AP⊥BP,AD⊥平面ABP,故AD⊥BP,于是BP⊥平面ADP,从而BP⊥AQ;
(2)由$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$得∠AO1P=60°,于是△AO1P是等边三角形,AP=2,在Rt△ADP中由勾股定理求出圆柱的高AD,代入体积公式.
解答 解:(1)∵AB是⊙O1直径,∴AP⊥BP,
∵AD⊥平面ABP,BP?平面ABP,
∴AD⊥BP,
又∵AD∩AP=A,AD?平面ADP,AP?平面ADP,
∴BP⊥平面ADP,∵AQ?平面ADP,
∴BP⊥AQ.
(2)∵$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,
∴∠AO1P=60°,又∵O1A=O1P,
∴△AO1P是等边三角形,
∴AP=O1A=2,
∵AD⊥平面ABP,AP?平面ABP
AD⊥AP,∴AD═$\sqrt{D{P}^{2}-A{P}^{2}}$=2$\sqrt{2}$,
∴V${\;}_{圆柱O{O}_{1}}$=πO1A2•AD=8$\sqrt{2}$π.
点评 本题考查了线面垂直的性质与判定,圆柱的体积计算,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
15.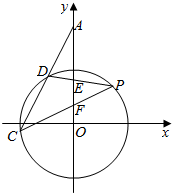 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
 如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )
如图,点P(3,4)为圆x2+y2=25的一点,点E,F为y轴上的两点,△PEF是以点P为顶点的等腰三角形,直线PE,PF交圆于D,C两点,直线CD交y轴于点A,则cos∠DAO的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{4}$ |
12.将函数y=$\sqrt{3}$sin2x的图象向右平移$\frac{π}{4}$个单位长度,再将所得图象的所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),得到的图象所对应的函数解析式为( )
| A. | y=$\sqrt{3}$sinx | B. | y=-$\sqrt{3}$cosx | C. | y=$\sqrt{3}$sin4x | D. | y=-$\sqrt{3}$cos4x |
16.平面上到点A(-5,0)、B(5,0)距离之和为10的点的轨迹是( )
| A. | 椭圆 | B. | 圆 | C. | 线段 | D. | 射线 |