题目内容
14.若$cos(\frac{π}{4}-θ)cos(\frac{π}{4}+θ)=\frac{{\sqrt{2}}}{6}$,则cos2θ=$\frac{{\sqrt{2}}}{3}$.分析 由两角和与差的余弦函数展开已知式子,由二倍角的余弦公式可得.
解答 解:∵$cos(\frac{π}{4}-θ)cos(\frac{π}{4}+θ)=\frac{{\sqrt{2}}}{6}$,
∴$\frac{\sqrt{2}}{2}$(cosθ+sinθ)•$\frac{\sqrt{2}}{2}$(cosθ-sinθ)=$\frac{\sqrt{2}}{6}$,
∴$\frac{1}{2}$(cos2θ-sin2θ)=$\frac{\sqrt{2}}{6}$,
∴$\frac{1}{2}$cos2θ=$\frac{\sqrt{2}}{6}$,
∴cos2θ=$\frac{\sqrt{2}}{3}$
故答案为:$\frac{\sqrt{2}}{3}$
点评 本题考查两角和与差的三角函数,涉及二倍角公式,属基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
5.若f(x)=ax3+x+c在[a,b]上是奇函数,则a+b+c+2的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
9.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且一个零点是2,则使得f(x)<0的x的取值范围是( )
| A. | (-∞,-2] | B. | (-∞,-2)∪(2,+∞) | C. | (2,+∞) | D. | (-2,2) |
19.若n∈N*,则1+2+22+23+…+2n+1=( )
| A. | A2n+1-1 | B. | 2n+2-1 | C. | $\frac{(n+2)(1+{2}^{n+1})}{2}$ | D. | $\frac{(n+1)(1+{2}^{n+1})}{2}$ |
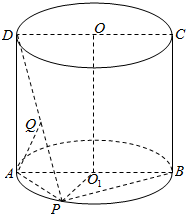 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在$\widehat{{A}{B}}$上且$\widehat{{A}{P}}=\frac{1}{3}\widehat{{A}{P}{B}}$,Q为PD上任意一点.