题目内容
 用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个无盖的圆锥形容器,如图,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要多少面积的铁皮?该容器的容积又是多少?(衔接部分忽略不计,结果精确到0.1cm2)分析:如图所示,由于PO⊥底面⊙O,该圆锥的母线与底面所在平面的夹角为45°,可得△AOP是等腰直角三角形,进而得到底面半径r=OP=10,AP=10
.再利用S侧面积=
×2πr•AP和V=
πr2•OP即可得出.
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:如图所示,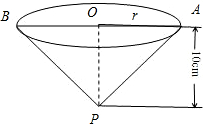
∵PO⊥底面⊙O,该圆锥的母线与底面所在平面的夹角为45°,
∴△AOP是等腰直角三角形,
∴底面半径r=OP=10,AP=10
.
∴S侧面积=
×2πr•AP=π×10×10
≈442.7.cm2
V=
πr2•OP=
π×102×10≈1046.7cm3.
答:制作该容器需要442.7cm2的铁皮,该容器的容积是1046.7cm3.

∵PO⊥底面⊙O,该圆锥的母线与底面所在平面的夹角为45°,
∴△AOP是等腰直角三角形,
∴底面半径r=OP=10,AP=10
| 2 |
∴S侧面积=
| 1 |
| 2 |
| 2 |
V=
| 1 |
| 3 |
| 1 |
| 3 |
答:制作该容器需要442.7cm2的铁皮,该容器的容积是1046.7cm3.
点评:熟练掌握圆锥的性质、侧面积和体积计算公式等是解题的关键.

练习册系列答案
相关题目
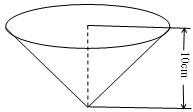 如图,用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要铁皮面积为
如图,用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在平面的夹角为45°,容器的高为10cm.制作该容器需要铁皮面积为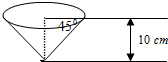 (2013•奉贤区二模)用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在的平面所成角为45°,容器的高为10cm,制作该容器需要
(2013•奉贤区二模)用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在的平面所成角为45°,容器的高为10cm,制作该容器需要 A.
A.