题目内容

设F1，F2是双曲线C：－＝1(a>0，b>0)的两个焦点，P是C上一点，若|PF1|＋|PF2|＝6a且△PF1F2的最小内角为30°，则双曲线C的离心率为________．

 

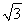
【解析】不妨设F1，F2分别为双曲线的左、右焦点，点P在双曲线的右支上，由双曲线的定义得

|PF1|－|PF2|＝2a，又|PF1|＋|PF2|＝6a，

求得|PF1|＝4a，|PF2|＝2a.

又在△PF1F2中，∠PF1F2＝30°，所以∠PF2F1＝90°，求得|F1F2|＝2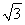a，故双曲线C的离心率e＝＝.

 

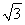练习册系列答案
相关题目

已知椭圆C：＋＝1(a＞b＞0)的左焦点为F，C与过原点的直线相交于A，B两点，连接AF，BF.若|AB|＝10，|BF|＝8，cos∠ABF＝，则C的离心率为________．

 

函数f(x)＝ln(x2＋1)的图象大致是 (　　)．

 

 

已知矩阵A＝，B＝，求矩阵A－1B.

 

某学校高一、高二、高三年级的学生人数之比为3∶3∶4，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取________名学生．

 

在平面直角坐标系xOy中，圆C的方程为x2＋y2－8x＋15＝0，若直线y＝kx－2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是________．

 

在等差数列{an}中，已知a8≥15，a9≤13，则a12的取值范围是________．

 

已知正数a，b，c满足：5c－3a≤b≤4c－a，cln b≥a＋cln c，则的取值范围是________．

 

已知点P(x，y)是直线kx＋y＋4＝0(k>0)上一动点，PA，PB是圆C：x2＋y2－2y＝0的两条切线，A，B为切点，若四边形PACB的最小面积是2，则k的值为________．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网