题目内容
1.已知函数f(x)=$\frac{1-x}{x}$+klnx,k<$\frac{1}{e}$,求函数f(x)在[$\frac{1}{e}$,e]上的最大值和最小值.分析 求函数的导数,判断函数的单调性,结合函数最值和单调性之间的关系进行求解即可.
解答 解:函数的定义域为(0,+∞),
则函数的导数f′(x)=$\frac{k}{x}$-$\frac{1}{{x}^{2}}$=$\frac{kx-1}{{x}^{2}}$=$\frac{k(x-\frac{1}{k})}{{x}^{2}}$,
若k≤0,则f′(x)≤0,即函数在[$\frac{1}{e}$,e]单调递减,则最大值为f($\frac{1}{e}$)=$\frac{1-\frac{1}{e}}{\frac{1}{e}}$+kln$\frac{1}{e}$=e-1-klne,
最小值为f(e)=$\frac{1-e}{e}$+k=$\frac{1}{e}$+k-1.
若k>0,则由f′(x)>0得x>$\frac{1}{k}$,此时函数单调递增,
由f′(x)<0得0<x<$\frac{1}{k}$,此时函数单调递减,
即当x=$\frac{1}{k}$时,函数取得极小值.
∵k<$\frac{1}{e}$,∴$\frac{1}{k}$>e,即函数f(x)在[$\frac{1}{e}$,e]单调递减,则最大值为f($\frac{1}{e}$)=$\frac{1-\frac{1}{e}}{\frac{1}{e}}$+kln$\frac{1}{e}$=e-1-klne,
最小值为f(e)=$\frac{1-e}{e}$+k=$\frac{1}{e}$+k-1.
综上函数f(x)的最大值为f($\frac{1}{e}$)=e-1-klne,最小值为f(e)=$\frac{1}{e}$+k-1.
点评 本题主要考查函数最值的求解,求函数的导数,判函数的单调性是解决本题的关键.

练习册系列答案
相关题目
11.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)与直线y=2x有交点,则双曲线离心率的取值范围是( )
| A. | ($\sqrt{5}$,+∞) | B. | [$\sqrt{5}$,+∞) | C. | (1,$\sqrt{5}$)∪($\sqrt{5}$,+∞) | D. | (1,$\sqrt{5}$) |
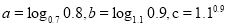 ,则
,则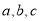 的大小关系是( )
的大小关系是( )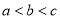 B.
B.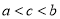
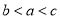 D.
D.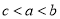
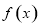 是定义在
是定义在 上的以4为周期的函数,当
上的以4为周期的函数,当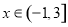 时,
时,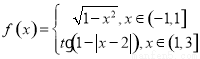 ,其中
,其中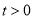 .若函数
.若函数 的零点个数是5,则
的零点个数是5,则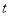 的取值范围为( )
的取值范围为( )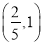 B.
B.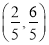 C.
C.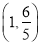 D.
D.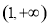
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.