题目内容
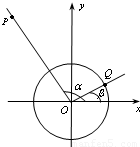
 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为 .
.
(Ⅰ)求sinα、cosβ;
(Ⅱ)若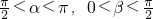 ,求α+β.
,求α+β.
解:(Ⅰ)根据三角函数的定义可知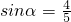 ,
,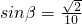 .(3分)
.(3分)
根据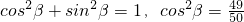 ,(4分)
,(4分)
又因为β的终边在第一象限,
所以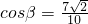 .(5分)
.(5分)
(Ⅱ)法一由(Ⅰ)可得,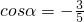 ,(6分)
,(6分)
∵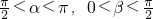 ,
,
∴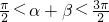 .(7分)
.(7分)
∵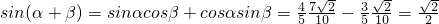 .(10分)
.(10分)
又∵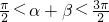 ,
,
∴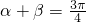 .(12分)
.(12分)
(Ⅱ)法二:由(Ⅰ)可得,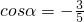 •
•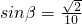 .(6分)
.(6分)
∵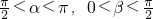 ,
,
∴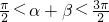 .(7分)
.(7分)
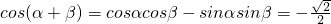 ,(10分)
,(10分)
又∵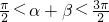 ,
,
∴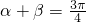 或
或 .
.
∵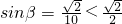 ,
,
∴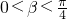 ,
,
∴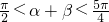 ,
,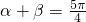 舍掉
舍掉
∴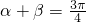 .(12分)
.(12分)
(注:另解中如果没有舍掉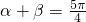 或者没有说明理由就舍掉
或者没有说明理由就舍掉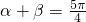 ,扣2分)
,扣2分)
分析:(Ⅰ)直接根据三角函数的定义,求出sinα、sinβ,然后再求cosβ;
(Ⅱ)法一由(Ⅰ)可得,cosα,求出α+β的正弦值,根据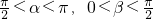 ,求出α+β.
,求出α+β.
法二求出α+β的余弦值,说明α+β的范围,然后求解即可.
点评:本题考查任意角的三角函数的定义,两角和与差的余弦函数,两角和与差的正弦函数,考查计算能力,是中档题.
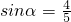 ,
,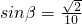 .(3分)
.(3分)根据
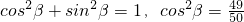 ,(4分)
,(4分)又因为β的终边在第一象限,
所以
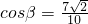 .(5分)
.(5分)(Ⅱ)法一由(Ⅰ)可得,
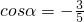 ,(6分)
,(6分)∵
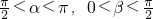 ,
,∴
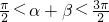 .(7分)
.(7分)∵
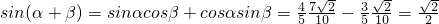 .(10分)
.(10分)又∵
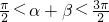 ,
,∴
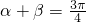 .(12分)
.(12分)(Ⅱ)法二:由(Ⅰ)可得,
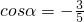 •
•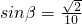 .(6分)
.(6分)∵
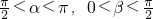 ,
,∴
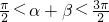 .(7分)
.(7分)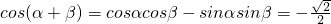 ,(10分)
,(10分)又∵
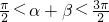 ,
,∴
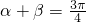 或
或 .
.∵
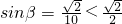 ,
,∴
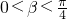 ,
,∴
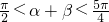 ,
,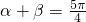 舍掉
舍掉∴
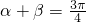 .(12分)
.(12分)(注:另解中如果没有舍掉
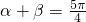 或者没有说明理由就舍掉
或者没有说明理由就舍掉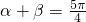 ,扣2分)
,扣2分)分析:(Ⅰ)直接根据三角函数的定义,求出sinα、sinβ,然后再求cosβ;
(Ⅱ)法一由(Ⅰ)可得,cosα,求出α+β的正弦值,根据
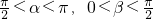 ,求出α+β.
,求出α+β.法二求出α+β的余弦值,说明α+β的范围,然后求解即可.
点评:本题考查任意角的三角函数的定义,两角和与差的余弦函数,两角和与差的正弦函数,考查计算能力,是中档题.

练习册系列答案
相关题目
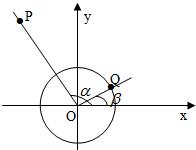 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为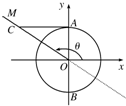 如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么?
如图所示,已知单位圆O与y轴交于A、B两点,角θ的顶点为原点,始边在x轴的非负半轴上,终边在射线OM上,过点A作直线AC垂直于y轴与角θ的终边OM交于点C,则有向线段AC表示的函数值是什么? 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
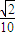 .
.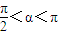 ,
,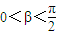 ,求α+β.
,求α+β.