题目内容
甲、乙、丙3人投篮,投进的概率分别是| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
(Ⅰ)3人都投进的概率;
(Ⅱ)3人中恰有2人投进的概率.
分析:本题考查的知识点是相互独立事件的概率乘法公式和加法公式,
(Ⅰ)记“甲投进“为事件A1,“乙投进“为事件A2,“丙投进“为事件A3,则3人都投中的概率为P(A1A2A3)=P(A1)•P(A2)•P(A3)代入计算即可得到答案.
(Ⅱ)3人中恰有2人投进分为三种情况,即甲未投进,乙和丙均投进,乙未投进,甲和丙均投进,丙未投进,甲和乙均投进,故3人中恰有2人投进的概率P(B)=P(
A2A3)+P(A1
A3)+P(A1A2
)=P(
)•P(A2)•P(A3)+P(A1)•P(
)•P(A3)+P(A1)•P(A2)•P(
)代入计算即可得到答案.
(Ⅰ)记“甲投进“为事件A1,“乙投进“为事件A2,“丙投进“为事件A3,则3人都投中的概率为P(A1A2A3)=P(A1)•P(A2)•P(A3)代入计算即可得到答案.
(Ⅱ)3人中恰有2人投进分为三种情况,即甲未投进,乙和丙均投进,乙未投进,甲和丙均投进,丙未投进,甲和乙均投进,故3人中恰有2人投进的概率P(B)=P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
解答:解:(Ⅰ)记“甲投进“为事件A1,“乙投进“为事件A2,“丙投进“为事件A3,
则P(A1)=
,P(A2)=
,P(A3)=
,
∴P(A1A2A3)=P(A1)•P(A2)•P(A3)=
×
×
=
∴3人都投进的概率为
(Ⅱ)设“3人中恰有2人投进“为事件B
P(B)=P(
A2A3)+P(A1
A3)+P(A1A2
)
=P(
)•P(A2)•P(A3)+P(A1)•P(
)•P(A3)+P(A1)•P(A2)•P(
)
=(1-
)×
×
+
×(1-
)×
+
×
×(1-
)=
∴3人中恰有2人投进的概率为
则P(A1)=
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
∴P(A1A2A3)=P(A1)•P(A2)•P(A3)=
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 15 |
∴3人都投进的概率为
| 1 |
| 15 |
(Ⅱ)设“3人中恰有2人投进“为事件B
P(B)=P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
=P(
. |
| A1 |
. |
| A2 |
. |
| A3 |
=(1-
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 10 |
∴3人中恰有2人投进的概率为
| 3 |
| 10 |
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
相关题目
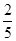 ,
, ,
, .
现3人各投篮1次,
.
现3人各投篮1次,