题目内容
甲、乙、丙3人投篮,投进的概率分别是
,
,
.
(1)现3人各投篮1次,求3人都没有投进的概率;
(2)用ξ表示乙投篮10次的进球数,求随机变量ξ的概率分布及数学期望Eξ和方差Dξ;
(3)若η=4ξ+1,求Eη和Dη.
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
(1)现3人各投篮1次,求3人都没有投进的概率;
(2)用ξ表示乙投篮10次的进球数,求随机变量ξ的概率分布及数学期望Eξ和方差Dξ;
(3)若η=4ξ+1,求Eη和Dη.
分析:(Ⅰ)分别记“甲、乙、丙投篮1次投进”为事件A1、A2、A3,“3人都没有投进”为事件A,由相互独立事件概率的乘法公式,计算可得答案;
(2)根据题意,随机变量ξ的可能值有0,1,2,3,进而由随机变量的概率分布与期望的计算方法,计算可得答案.
(3)由已知η=4ξ+1,根据方差的性质求得η的均值、方差即可.
(2)根据题意,随机变量ξ的可能值有0,1,2,3,进而由随机变量的概率分布与期望的计算方法,计算可得答案.
(3)由已知η=4ξ+1,根据方差的性质求得η的均值、方差即可.
解答:解:(1)记“甲投篮1次投进”为事件A1,“乙投篮1次投进”为事件A2,“丙投篮1次投进”为事件A3,
“3人都没有投进”为事件A.
则P(A1)=
,P(A2)=
,P(A3)=
,
∴P(A)=(
)
=P (
)•(
)•(
)
=[1-P(A1)]•[1-P(A2)]•[1-P(A3)]
=(1-
)(1-
)(1-
)
=
∴3人都没有投进的概率为
.
(2)随机变量ξ的可能值有0,1,2,3,…,10.
ξ~B(10,
),
P(ξ=k)=C10k(
)k(
)10-k(k=0,1,2,…,10),
Eξ=np=10×
=4.
方差Dξ=np(1-p)=10×
×
=
.
(3)若η=4ξ+1,由(2)得,
Eη=E(4ξ+1)=4Eξ+1=4×4+1=17
Dη=D(4ξ+1)=42Dξ=16×
=
.
“3人都没有投进”为事件A.
则P(A1)=
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
∴P(A)=(
. |
| A1 |
. |
| A2 |
. |
| A3 |
=P (
. |
| A1 |
. |
| A2 |
. |
| A3 |
=[1-P(A1)]•[1-P(A2)]•[1-P(A3)]
=(1-
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
=
| 1 |
| 5 |
∴3人都没有投进的概率为
| 1 |
| 5 |
(2)随机变量ξ的可能值有0,1,2,3,…,10.
ξ~B(10,
| 2 |
| 5 |
P(ξ=k)=C10k(
| 2 |
| 5 |
| 3 |
| 5 |
Eξ=np=10×
| 2 |
| 5 |
方差Dξ=np(1-p)=10×
| 2 |
| 5 |
| 3 |
| 5 |
| 12 |
| 5 |
(3)若η=4ξ+1,由(2)得,
Eη=E(4ξ+1)=4Eξ+1=4×4+1=17
Dη=D(4ξ+1)=42Dξ=16×
| 12 |
| 5 |
| 192 |
| 5 |
点评:本题考查相互独立事件的概率的乘法公式与随机变量的概率分布及数学期望的计算,能力上考查学生的分析问题、解决问题的能力,是高考热点.

练习册系列答案
相关题目
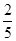 ,
, ,
, .
现3人各投篮1次,
.
现3人各投篮1次,