题目内容
已知过点M(-3,-3)的直线l被圆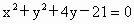 所截得的弦长为
所截得的弦长为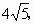 求直线l的方程.
求直线l的方程.
答案:x+2y+9=0$2x-y+3=0
解析:
解析:
|
解:将圆的方程写成标准形式,得 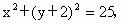
如图所示,因为直线 l被圆所截得的弦长是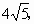 所以弦心距为 所以弦心距为
即圆心到所求直线 l的距离为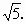
因为直线 l过点M(―3,―3),易见,当直线l与x轴垂直时不合题意,∴斜率存在,所以可设所求直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.根据点到直线的距离公式,得到圆心到直线 l的距离
因此, 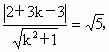 即 即
两边平方,并整理得到 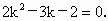 解得 解得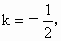 或k=2. 或k=2.
所以,所求直线 l有两条,方程分别为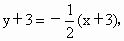 或 或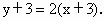 即 即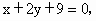 或 或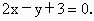
已知直线被圆截得的弦长,可从两个方向建立关系式;一是几何关系,即由弦心距、半弦、半径组成一个直角三角形;二是代数关系,借助于弦长公式建立关系式. |

练习册系列答案
相关题目

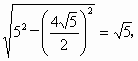

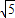 ,则直线l的方程是 .
,则直线l的方程是 .