题目内容
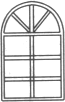
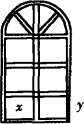
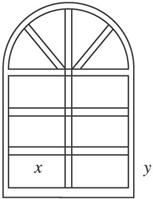
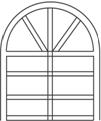
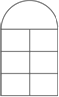
有L米长的钢材，要做成如图所示的窗架，上半部分是半圆，下半部分为6个全等的小长方形组成的长方形，试问小长方形的长、宽为多少时窗户所通过的光线最多？求窗户面积的最大值．
答案：
解析：
提示：
解析：
解：如图所示，设小长方形的长为x，宽为y，窗户的面积为S，则由图形条件可得8x＋πx＋9y＝L，所以，9y＝L－(8＋π)x．
S＝
＋6xy＝
＋
[Lx－(8＋π)x2]
＝
6(x
)2＋
(0＜x＜
)．
要使窗户所通过的光线最多，即要窗户的面积最大．
所以，当x＝
时，S有最大值为
．
此时，y＝
．
即当x＝，y＝
时，窗户所通过的光线最多．此时，窗户面积的最大值为
．
提示：
窗户所通过的光线最多，则要求窗户面积的最大值．本题先求小长方形的长与窗户面积的函数关系式，再求函数的最值．
练习册系列答案
阅读快车系列答案
相关题目
