题目内容
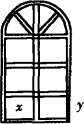
有l m长的钢材，要做成如图所示的窗架，上半部分为半圆，下半部分为六个全等小矩形组成的矩形.试问小矩形的长、宽比为多少时，窗所通过的光线最多？并具体算出窗框面积的最大值.
提示：设小矩形长为x，宽为y，则由图形条件可得11x+πx+9y=l. ∴9y=l-（11+π）x. 要使窗所通过的光线最多，即要窗框面积最大，则 S= 所以当x= 即 窗框面积S有最大值，Smax=
+6xy=
x2+
［lx-（11+π）x2］=-
时（x∶y=18∶（22-π）≈1∶1），
.
练习册系列答案
新课标学案高考调研系列答案
凤凰新学案系列答案
名师特攻百分好题测评卷系列答案
单元加期末100分冲刺卷系列答案
单元月考期末测评卷系列答案
新课堂单元测试卷系列答案
钟书金牌一卷夺冠系列答案
名师优选冲刺卷系列答案
创新学习同步解析与测评系列答案
相关题目
