题目内容
函数f(x)= ,x∈[2,4]的最小值是
,x∈[2,4]的最小值是
- A.3
- B.4
- C.5
- D.6
A
分析:由函数f(x)= ,我们易求出函数的导函数f'(x),根据导数法我们易计算出函数在区间[2,4]上的单调性,根据单调性我们易得到函数最小值.
,我们易求出函数的导函数f'(x),根据导数法我们易计算出函数在区间[2,4]上的单调性,根据单调性我们易得到函数最小值.
解答:因为f(x)= =2+
=2+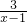 ;
;
∴f′(x)=-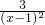 ;
;
当x∈[2,4]时,f'(x)<0恒成立
故f(x)= 在区间[2,4]上是减函数,
在区间[2,4]上是减函数,
∴函数f(x)= 在区间[2,4]上最小值为f(4)=3.
在区间[2,4]上最小值为f(4)=3.
故选:A.
点评:本题考查的知识点是函数的单调性的应用,函数单调性的主要应用为解不等式,求最值及比较数的大小,本题中利用法确定函数的单调性是解答的关键.
分析:由函数f(x)=
 ,我们易求出函数的导函数f'(x),根据导数法我们易计算出函数在区间[2,4]上的单调性,根据单调性我们易得到函数最小值.
,我们易求出函数的导函数f'(x),根据导数法我们易计算出函数在区间[2,4]上的单调性,根据单调性我们易得到函数最小值.解答:因为f(x)=
 =2+
=2+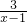 ;
;∴f′(x)=-
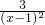 ;
;当x∈[2,4]时,f'(x)<0恒成立
故f(x)=
 在区间[2,4]上是减函数,
在区间[2,4]上是减函数,∴函数f(x)=
 在区间[2,4]上最小值为f(4)=3.
在区间[2,4]上最小值为f(4)=3.故选:A.
点评:本题考查的知识点是函数的单调性的应用,函数单调性的主要应用为解不等式,求最值及比较数的大小,本题中利用法确定函数的单调性是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目