题目内容
(本小题满分10分)已知二次函数f(x)满足:①在x=1时有极值;②图象过点(0,-3),且在该点处的切线与直线2x+y=0平行.
⑴求f(x)的解析式;
⑵求函数g(x)=f(x2)的单调递增区间.
【答案】
解:⑴设f(x)=ax2+bx+c,则f ¢(x)=2ax+b.
由题设可得: 即
即 解得
解得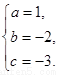
所以f(x)=x2-2x-3.
⑵g(x)=f(x2)=x4-2x2-3,g ¢(x)=4x3-4x=4x(x-1)(x+1).列表:
|
x |
(-∞,-1) |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
(1,+∞) |
|
f¢(x) |
- |
0 |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↘ |
|
↗ |
|
↘ |
|
↗ |
由表可得:函数g(x)的单调递增区间为(-1,0),(1,+∞).
【解析】略

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
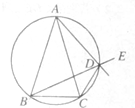 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.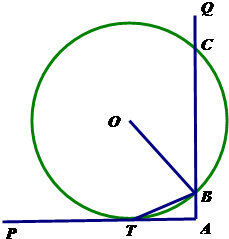 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,