题目内容
(本小题满分10分)
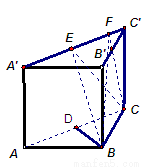
如图,在直三棱柱 中,
中, ,
, .棱
.棱 上有两个动点E,F,且EF =" a" (a为常数).
上有两个动点E,F,且EF =" a" (a为常数).

(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
【答案】
(Ⅰ)取AC中点D,连接BD,直线BD即为所求直线(Ⅱ)体积是定值为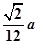
【解析】
试题分析:(Ⅰ)取AC中点D,连接BD.
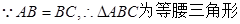 ,D为底边AC中点,∴
,D为底边AC中点,∴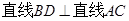 .
.
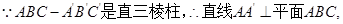
∵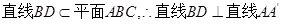 .
.
又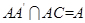 ,∴直线
,∴直线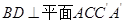 .
.
∵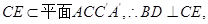
∴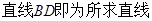 .
------5分
.
------5分
(Ⅱ)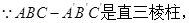 直线
直线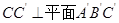 ,
,
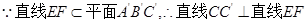 .
.
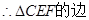 EF上的高为线段
EF上的高为线段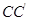 ,
,
由已知条件得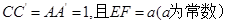 ,
,
故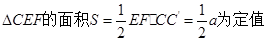
由(Ⅰ)可知,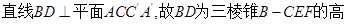 .
.
在等腰三角形ABC中,可求得BD=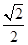 ,
,
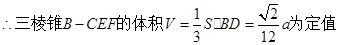 .------10分
.------10分
考点:线面垂直的判定和性质定理及锥体的体积计算
点评:线面垂直的判定:一条直线垂直于平面内两条相交直线,则这条直线垂直于平面。锥体的底面积为S,高为h,则体积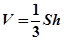

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,