题目内容
3．化简：（1）$\frac{{a}^{-1}+{b}^{-1}}{（ab）^{-1}}$；
（2）$\frac{{a}^{\frac{4}{3}}-8{a}^{\frac{1}{3}}b}{4{b}^{\frac{2}{3}}+2\root{3}{ab}+{a}^{\frac{2}{3}}}$÷（1-2$\root{3}{\frac{b}{a}}$）•$\root{3}{a}$．
分析 （1）（2）利用指数幂的运算性质、乘法公式即可得出．
解答 解：（1）原式=$\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{ab}}$=a+b；
（2）原式=$\frac{{a}^{\frac{1}{3}}（{a}^{\frac{1}{3}}-（2b）^{\frac{1}{3}}）（{a}^{\frac{2}{3}}+2\root{3}{ab}+4{b}^{\frac{2}{3}}）}{4{b}^{\frac{2}{3}}+2\root{3}{ab}+{a}^{\frac{2}{3}}}$×$\frac{\root{3}{a}}{\root{3}{a}-2\root{3}{b}}$$•\root{3}{a}$
=a．
点评 本题考查了指数幂的运算性质、乘法公式，考查了计算能力，属于中档题．
练习册系列答案
相关题目
14．已知f（x）是定义在R上的奇函数，当0≤x≤1时，f（x）=x2，当x＞0时，f（x+1）=f（x）+f（1），若直线y=kx与函数y=f（x）的图象恰有11个不同的公共点，则实数k的取值范围为（ ）
| A． | （2$\sqrt{2}$-2，2$\sqrt{6}$-4） | B． | （$\sqrt{3}$+2，$\sqrt{3}$+$\sqrt{6}$） | C． | （2$\sqrt{2}$+2，2$\sqrt{6}$+4） | D． | （2$\sqrt{6}$-4，4$\sqrt{3}$-6） |
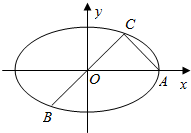如图所示，已知A、B、C是长轴为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且AC⊥BC，|BC|=2|AC|．
8．在△ABC中，角$C=\frac{π}{3}$，边AB=1，则△ABC周长的取值范围是（ ）
| A． | （2，3] | B． | [1，3] | C． | （0，2] | D． | （2，5] |