题目内容
给出下列命题:
①半径为2,圆心角的弧度数为
的扇形面积为
;
②若α、β为锐角,tan(α+β)=
,tan β=
,则α+2β=
;
③函数y=cos(2x-
)的一条对称轴是x=
π;
④?=
π是函数y=sin(2x+?)为偶函数的一个充分不必要条件.
其中真命题的序号是
①半径为2,圆心角的弧度数为
| 1 |
| 2 |
| 1 |
| 2 |
②若α、β为锐角,tan(α+β)=
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
③函数y=cos(2x-
| π |
| 3 |
| 2 |
| 3 |
④?=
| 3 |
| 2 |
其中真命题的序号是
②③④
②③④
.分析:①由扇形的面积公式S=
α•r2可求
②由α、β为锐角,tan(α+β)=
<1,tan β=
<1,可得0<α+β<
,0<β<
,,进而可得0<α+2β<
,然后利用tan(α+2β)=tan[(α+β)+β]=
可求
③根据函数对称轴处取得最值的性质可判断
④∅=
时,函数y=sin(2x+?)=-cos2x为偶函数,但是当y=sin(2x+?)为偶函数时,kπ+
π=∅,
| 1 |
| 2 |
②由α、β为锐角,tan(α+β)=
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| tan(α+β)+tanβ |
| 1-tan(α+β)tanβ |
③根据函数对称轴处取得最值的性质可判断
④∅=
| 3π |
| 2 |
| 1 |
| 2 |
解答:解:①由扇形的面积公式可得S=
×
×22=1,则半径为2,圆心角的弧度数为
的扇形面积为1;故①错误
②由α、β为锐角,tan(α+β)=
<1,tan β=
<1,可得0<α+β<
,0<β<
,
∴0<α+2β<
则tan(α+2β)=tan[(α+β)+β]=
=
=1
∴α+2β=
;故②正确
③当x=
时,函数y=cos(2x-
)=cosπ=-1取得函数的最小值,根据函数对称轴处取得最值的性质可知,函数的一条对称轴是x=
π;③正确
④∅=
时,函数y=sin(2x+?)=-cos2x为偶函数,但是当y=sin(2x+?)为偶函数时,kπ+
π=∅,即∅=
是函数y=sin(2x+?)为偶函数时的一个充分不必要条件.④正确
故答案为:②③④
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②由α、β为锐角,tan(α+β)=
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 4 |
| π |
| 4 |
∴0<α+2β<
| π |
| 2 |
则tan(α+2β)=tan[(α+β)+β]=
| tan(α+β)+tanβ |
| 1-tan(α+β)tanβ |
| ||||
1-
|
∴α+2β=
| π |
| 4 |
③当x=
| 2π |
| 3 |
| π |
| 3 |
| 2 |
| 3 |
④∅=
| 3π |
| 2 |
| 1 |
| 2 |
| 3π |
| 2 |
故答案为:②③④
点评:本题以命题的真假关系的判断为载体,主要考查了扇形的面积公式、两角和的正切公式、正弦函数与余弦函数的对称性质等知识的综合应用,此类试题综合性强,考查的知识点较多.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
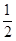 的扇形面积为
的扇形面积为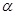 、
、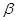 为锐角,
为锐角,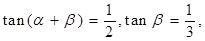 则
则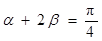 ;
;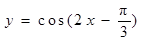 的一条对称轴是
的一条对称轴是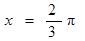 ;
;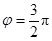 是函数
是函数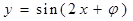 为偶函数的一个充分不必要条件.
为偶函数的一个充分不必要条件. 的扇形面积为
的扇形面积为 ;
; ,tan β=
,tan β= ,则α+2β=
,则α+2β=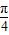 ;
;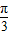 )的一条对称轴是x=
)的一条对称轴是x=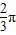 ;
;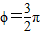 是函数y=sin(2x+ϕ)为偶函数的一个充分不必要条件.
是函数y=sin(2x+ϕ)为偶函数的一个充分不必要条件.