题目内容
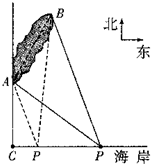 如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4
如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4| 3 |
(1)设CP=x,∠APB=θ,试将tanθ表示成x的函数;
(2)若要求在监测站P处观察全岛所张的视角最大,问点P应选址何处?
分析:(1)分别以直线CP,CA为x,y轴建立直角坐标系,过点B分别作CP,CA的垂线,垂足为D,E.由题设AB=4.5,AC=4
,∠BAE=30°,从而可求出A,B的坐标,又点P(x,0),从而可得tanθ表示成x的函数
(2)令x+4=t,则tanθ=
=
(t>4),利用基本不等式,可求tanθ的最大值.
| 3 |
(2)令x+4=t,则tanθ=
9
| ||
| 4t2-41t+400 |
9
| ||
4(t+
|
解答:解:(1)分别以直线CP,CA为x,y轴建立直角坐标系,过点B分别作CP,CA的垂线,垂足为D,E
由题设AB=4.5,AC=4
,∠BAE=30°,则CD=EB=4.5sin30°=
,AE=4.5×cos30°=
BD=EC=AE+AC=
∴A(0,4
),B(
,
)
又点P(x,0),则kPA=-
,kPB=-
(x≠
)
所以当x>0,且x≠
时,tanθ=
=
当x=
时,点P与点D重合,tanθ=tan∠CAD=
=
,满足上式,
所以tanθ=
(x>0)
(2)令x+4=t,则tanθ=
=
(t>4)
∵t+
≥2
=20,∴tanθ≤
=
当且仅当t=
>4,即t=10
∴x=6时取等号,此时tanθ取最大值
,θ取最大值.
答:点P应选址在点C正东方向6km处.
由题设AB=4.5,AC=4
| 3 |
| 9 |
| 4 |
9
| ||
| 4 |
BD=EC=AE+AC=
25
| ||
| 4 |
∴A(0,4
| 3 |
| 9 |
| 4 |
25
| ||
| 4 |
又点P(x,0),则kPA=-
4
| ||
| x |
25
| ||
| 4x-9 |
| 9 |
| 4 |
所以当x>0,且x≠
| 9 |
| 4 |
| kPA-kPB |
| 1+kPAkPB |
9
| ||
| 4x2-9x+300 |
当x=
| 9 |
| 4 |
| CD |
| AC |
3
| ||
| 16 |
所以tanθ=
9
| ||
| 4x2-9x+300 |
(2)令x+4=t,则tanθ=
9
| ||
| 4t2-41t+400 |
9
| ||
4(t+
|
∵t+
| 100 |
| t |
t•
|
9
| ||
| 80-41 |
3
| ||
| 13 |
当且仅当t=
| 100 |
| t |
∴x=6时取等号,此时tanθ取最大值
3
| ||
| 13 |
答:点P应选址在点C正东方向6km处.
点评:本题以实际问题为载体,考查三角函数模型的构建,考查基本不等式的运用,解题的关键是正确运用差角的正切公式及基本不等式.

练习册系列答案
相关题目
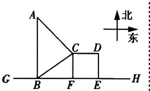 如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.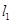 排水管,在路南侧沿直线
排水管,在路南侧沿直线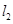 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将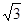 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为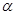 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.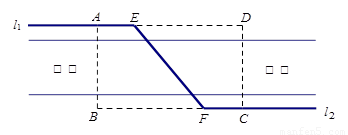
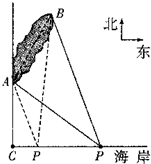 如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4
如图,在一条东西方向的海岸线上的点C处有一个原子能研究所,海岸线北侧有一个小岛,岛上建有一个核电站,该岛的一个端点A位于点C的正北方向4 km处,另一个端点B位于点A北偏东30°方向,且与点A相距4.5km,研究所拟在点C正东方向海岸线上的P处建立一个核辐射监测站.
km处,另一个端点B位于点A北偏东30°方向,且与点A相距4.5km,研究所拟在点C正东方向海岸线上的P处建立一个核辐射监测站. km处,另一个端点B位于点A北偏东30°方向,且与点A相距4.5km,研究所拟在点C正东方向海岸线上的P处建立一个核辐射监测站.
km处,另一个端点B位于点A北偏东30°方向,且与点A相距4.5km,研究所拟在点C正东方向海岸线上的P处建立一个核辐射监测站.