题目内容
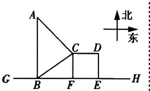 如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.
如图所示,GH是一条东西方向的公路,现准备在点B的正北方向的点A处建一仓库,设AB=y千米,并在公路旁边建造边长为x千米的正方形无顶中转站CDEF(其中边EF在公路GH上),现向公路和中转站分别修两条简易公路AB,AC,已知AB=AC+1,且∠ABC=60°.
(1)求y关于x的函数解析式;
(2)如果中转站四周围墙造价为l0万元/千米,公路造价为30万元/千米,问x取何值时,建中转站和道路总造价M最低.
解:(1)∵AB=y,AB=AC+1,∴AC=y-1.
在直角三角形BCF中,∵CF=x,∠ABC=60°,
∴∠CBF=30°,BC=2x.
由于2x+y-1>y,得 .
.
在△ABC中,∵AC2=AB2+BC2-2AB•BC•cos60°,
∴(y-1)2=y2+4x2-2xy
∴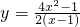
∵y>0, ,∴x>1
,∴x>1
∴y关于x的函数解析式是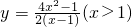 ;
;
(2)M=30(2y-1)+40x=10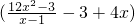
令x-1=t,则M=10(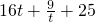 )≥490
)≥490
当且仅当t= ,x=
,x= ,
,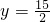 时,总造价M最低.
时,总造价M最低.
分析:(1)先求出BC,再在△ABC中,利用余弦定理,即可得到y关于x的函数解析式;
(2)确定建中转站和道路总造价解析式,利用换元法,结合基本不等式,即可得到结论.
点评:本题考查函数解析式,考查函数的最值,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.
在直角三角形BCF中,∵CF=x,∠ABC=60°,
∴∠CBF=30°,BC=2x.
由于2x+y-1>y,得
 .
.在△ABC中,∵AC2=AB2+BC2-2AB•BC•cos60°,
∴(y-1)2=y2+4x2-2xy
∴
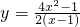
∵y>0,
 ,∴x>1
,∴x>1∴y关于x的函数解析式是
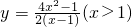 ;
;(2)M=30(2y-1)+40x=10
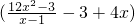
令x-1=t,则M=10(
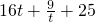 )≥490
)≥490当且仅当t=
 ,x=
,x= ,
,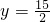 时,总造价M最低.
时,总造价M最低.分析:(1)先求出BC,再在△ABC中,利用余弦定理,即可得到y关于x的函数解析式;
(2)确定建中转站和道路总造价解析式,利用换元法,结合基本不等式,即可得到结论.
点评:本题考查函数解析式,考查函数的最值,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目