题目内容
【题目】已知函数![]() ,设直线
,设直线![]() 分别是曲线
分别是曲线![]() 的两条不同的切线;
的两条不同的切线;
(1)若函数![]() 为奇函数,且当
为奇函数,且当![]() 时,
时,![]() 有极小值为-4;
有极小值为-4;
(i)求![]() 的值;
的值;
(ii)若直线![]() 亦与曲线
亦与曲线![]() 相切,且三条不同的直线
相切,且三条不同的直线![]() 交于点
交于点![]() ,求实数m的取值范围;
,求实数m的取值范围;
(2)若直线![]() ,直线
,直线![]() 与曲线
与曲线![]() 切于点B且交曲线
切于点B且交曲线![]() 于点D,直线
于点D,直线![]() 与曲线
与曲线![]() 切于点C且交曲线
切于点C且交曲线![]() 于点A,记点
于点A,记点![]() 的横坐标分别为
的横坐标分别为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]()
![]() ;
;![]()
![]() ; (2)
; (2)![]() .
.
【解析】
(1)![]() 根据奇函数
根据奇函数![]() 和
和![]() 求得
求得![]() ;又
;又![]() ,求得
,求得![]() 和
和![]() ;
;![]() 假设切点和切线方程,根据极大值点为
假设切点和切线方程,根据极大值点为![]() 可确定一条切线为
可确定一条切线为![]() ;将
;将![]() 代入切线方程可得:
代入切线方程可得:![]() 和
和![]() ,从而可得
,从而可得![]() 的两根为
的两根为![]() ,构造函数
,构造函数![]() ,结合
,结合![]() 图像求得
图像求得![]() 的范围;(2)根据
的范围;(2)根据![]() 可得
可得![]() ,从而
,从而![]() ;将切线代入
;将切线代入![]() 求解出
求解出![]() ,从而得到
,从而得到![]() .
.
(1)![]()
![]() 是奇函数,且
是奇函数,且![]()
![]() 且
且![]() ,即
,即![]()
![]()
![]()
而当![]() 时有极小值
时有极小值![]()
![]()
![]()
![]()
![]()
经检验![]() 满足题意,则
满足题意,则![]()
![]() 设
设![]() 是曲线
是曲线![]() 上的一点
上的一点
由![]() 知:
知:![]() ,
,![]()
![]() 过
过![]() 点的切线方程为:
点的切线方程为:![]()
消去![]()
由此切线方程形式可知:过某一点的切线最多有三条;
又由奇函数性质可知:点![]() 是极大值点
是极大值点
从而![]() 是一条切线且过点
是一条切线且过点![]()
再设另两条切线的切点为![]() 、
、![]() ,其中
,其中![]()
则可令切线![]() ,
,![]()
将![]() 代入
代入![]() 的方程中
的方程中
化简可得:![]() 且
且![]()
从而有:![]() 且
且![]()
![]() 是方程
是方程![]() 的两根
的两根
构造函数:![]()
![]()
由![]() 得:
得:![]() 或
或![]()
而![]() ,
,![]() ,结合图象:
,结合图象:
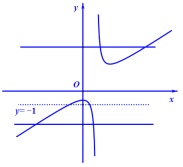
可得:实数![]() 的取值范围是:
的取值范围是:![]()
(2)令![]() ,
,![]() ;由
;由![]() 及
及![]()
可得:![]()
而![]() ,化简可得:
,化简可得:![]() ,即
,即![]()
将切线![]() 的方程
的方程![]() 代入
代入![]() 中并化简得:
中并化简得:
![]() ,即
,即![]()
![]() ;同理:
;同理:![]()
则![]() ,
,![]() ,
,![]()
![]()

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目




