题目内容
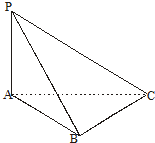 (2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,
(2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,(1)证明:平面PAB⊥平面PBC;
(2)若PA=
| 6 |
2
| ||
| 3 |
分析:(1)由PA⊥面ABC,知PA⊥BC,由AB⊥BC,且PA∩AB=A,知BC⊥面PAB,由此能够证明面PAB⊥面PBC.
(2)法一:过A作AE⊥PB于E,过E作EF⊥PC于F,连接AF,得到∠EFA为B-PC-A的二面角的平面角.由此能求出二面角B-PC-A的大小.
法二:由AB=
,BC=1,以BA为x轴,BC为y轴,建立空间直角坐标系,利用向量法能求出二面角B-PC-A的大小.
(2)法一:过A作AE⊥PB于E,过E作EF⊥PC于F,连接AF,得到∠EFA为B-PC-A的二面角的平面角.由此能求出二面角B-PC-A的大小.
法二:由AB=
| 2 |
解答: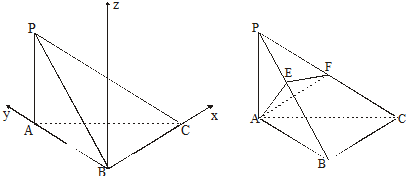 (1)证明:∵PA⊥面ABC,∴PA⊥BC,
(1)证明:∵PA⊥面ABC,∴PA⊥BC,
∵AB⊥BC,且PA∩AB=A,
∴BC⊥面PAB
而BC?面PBC中,∴面PAB⊥面PBC.…(5分)
(2)解法一:过A作AE⊥PB于E,过E作EF⊥PC于F,连接AF,如图所示
则∠EFA为B-PC-A的二面角的平面角 …(8分)
由PA=
,在Rt△PBC中,cos∠COB=
.
Rt△PAB中,∠PBA=60°.
∴AB=
,PB=2
,PC=3
∴AE=
=
同理:AF=
…(10分)
∴sin∠EFA=
,…(11分)
∴∠EFA=60.…(12分)
解法二:向量法:由题可知:AB=
,BC=1,
建立如图所示的空间直角坐标系…(7分)
B(0,0,0),C(1,0,0),A(0,
,0),P(0,
,
),
假设平面BPC的法向量为
=(x1,y1,z1),
∴
取z1=
可得平面BPC的法向量为
=(0,-3
,
)…(9分)
同理PCA的法向量为
=(2,-
,0)…(11分)
∴cos<
,
>=
=
,∴所求的角为60°.…(12分)
 (1)证明:∵PA⊥面ABC,∴PA⊥BC,
(1)证明:∵PA⊥面ABC,∴PA⊥BC,∵AB⊥BC,且PA∩AB=A,
∴BC⊥面PAB
而BC?面PBC中,∴面PAB⊥面PBC.…(5分)
(2)解法一:过A作AE⊥PB于E,过E作EF⊥PC于F,连接AF,如图所示
则∠EFA为B-PC-A的二面角的平面角 …(8分)
由PA=
| 6 |
| 2 |
| 3 |
| 2 |
Rt△PAB中,∠PBA=60°.
∴AB=
| 2 |
| 2 |
∴AE=
| PA•AB |
| PB |
| ||
| 2 |
同理:AF=
| 2 |
∴sin∠EFA=
| ||
| 2 |
∴∠EFA=60.…(12分)
解法二:向量法:由题可知:AB=
| 2 |
建立如图所示的空间直角坐标系…(7分)
B(0,0,0),C(1,0,0),A(0,
| 2 |
| 2 |
| 6 |
假设平面BPC的法向量为
| n |
∴
|
取z1=
| 6 |
| n |
| 2 |
| 6 |
同理PCA的法向量为
| m |
| 2 |
∴cos<
| m |
| n |
| ||||
|
|
| 1 |
| 2 |
点评:本题考查平面与平面垂直的证明,考查二面角的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
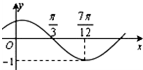 (2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )
(2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )