题目内容
(2013•东坡区一模)若对于定义在R上的函数f(x),其图象是连续不断的,且存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立,则称f(x) 是一个“λ-伴随函数”.有下列关于“λ-伴随函数”的结论:
①f(x)=0 是常数函数中唯一个“λ-伴随函数”;
②f(x)=x不是“λ-伴随函数”;
③f(x)=x2是一个“λ-伴随函数”;
④“
-伴随函数”至少有一个零点.
其中不正确的序号是
①f(x)=0 是常数函数中唯一个“λ-伴随函数”;
②f(x)=x不是“λ-伴随函数”;
③f(x)=x2是一个“λ-伴随函数”;
④“
| 1 | 2 |
其中不正确的序号是
①③
①③
(填上所有不正确的结论序号).分析:①设f(x)=C是一个“λ-伴随函数”,则(1+λ)C=0,当λ=-1时,可以取遍实数集,因此f(x)=0不是唯一一个常值“λ-伴随函数”;
②根据f(x)=x,可得f(x+λ)+λf(x)=x+λ+λx,故不存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立;
③用反证法,假设f(x)=x2是一个“λ-伴随函数”,则(x+λ)2+λx2=0,从而有λ+1=2λ=λ2=0,此式无解;
④令x=0,可得f(
)=-
f(0),若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f(
)•f(0)=-
(f(0))2<0,由此可得结论.
②根据f(x)=x,可得f(x+λ)+λf(x)=x+λ+λx,故不存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立;
③用反证法,假设f(x)=x2是一个“λ-伴随函数”,则(x+λ)2+λx2=0,从而有λ+1=2λ=λ2=0,此式无解;
④令x=0,可得f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①设f(x)=C是一个“λ-伴随函数”,则(1+λ)C=0,当λ=-1时,可以取遍实数集,因此f(x)=0不是唯一一个常值“λ-伴随函数”,故①不正确;
②∵f(x)=x,∴f(x+λ)+λf(x)=x+λ+λx,当λ=-1时,f(x+λ)+λf(x)=-1≠0;λ≠-1时,f(x+λ)+λf(x)=0有唯一解,∴不存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立,∴(x)=x不是“λ-伴随函数”,故②正确;
③用反证法,假设f(x)=x2是一个“λ-伴随函数”,则(x+λ)2+λx2=0,即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“λ-伴随函数”,故③不正确;
④令x=0,得f(
)+
f(0)=0,所以f(
)=-
f(0)
若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f(
)•f(0)=-
(f(0))2<0.
又因为f(x)的函数图象是连续不断,所以f(x)在(0,
)上必有实数根.因此任意的“
-伴随函数”必有根,即任意“
-伴随函数”至少有一个零点,故④正确
故答案为:①③
②∵f(x)=x,∴f(x+λ)+λf(x)=x+λ+λx,当λ=-1时,f(x+λ)+λf(x)=-1≠0;λ≠-1时,f(x+λ)+λf(x)=0有唯一解,∴不存在常数λ(λ∈R)使得f(x+λ)+λf(x)=0对任意实数x都成立,∴(x)=x不是“λ-伴随函数”,故②正确;
③用反证法,假设f(x)=x2是一个“λ-伴随函数”,则(x+λ)2+λx2=0,即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“λ-伴随函数”,故③不正确;
④令x=0,得f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f(
| 1 |
| 2 |
| 1 |
| 2 |
又因为f(x)的函数图象是连续不断,所以f(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:①③
点评:本题考查的知识点是函数的概念及构成要素,函数的零点,正确理解f(x)是λ-伴随函数的定义,是解答本题的关键.

练习册系列答案
相关题目
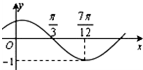 (2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )
(2013•东坡区一模)函数f(x)=Asin(ωx+?)的图象如下图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象 ( )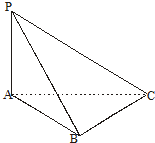 (2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,
(2013•东坡区一模)三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,