题目内容
（本小题满分10分）选修4－4：坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点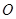
处，极轴与
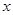轴的正半轴重合，且长度单位相同．圆
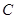的参数方程为
(
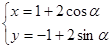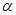为参数),点
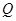的极坐标为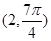
. （1）化圆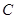的参数方程为极坐标方程；
（2）若点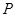
是圆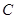上的任意一点, 求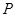,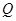两点间距离的最小值．
已知极坐标的极点在平面直角坐标系的原点
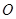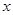处，极轴与轴的正半轴重合，且长度单位相同．圆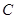的参数方程为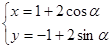(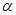为参数),点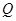的极坐标为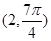. （1）化圆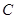的参数方程为极坐标方程；（2）若点
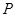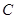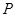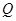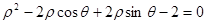是圆上的任意一点, 求,两点间距离的最小值．（Ⅰ）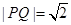
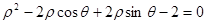（Ⅱ）
（Ⅱ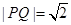）试题分析：（1）圆C的直角坐标方程为
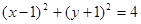，展开得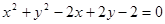
化为极坐标方程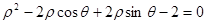（2）点Q的直角坐标为
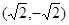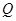，且点在圆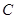内，由（1）知点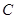的直角坐标为
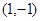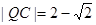所以
，所以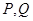
两点间距离的最小值为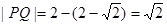
点评：第二小题中首先求圆心到定点的距离，再利用圆的对称性求解
练习册系列答案
中考解读考点精练系列答案
相关题目
）（
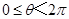）中，曲线
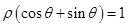与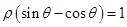
的交点的极坐标为 .
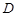的极坐标是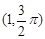
，曲线C的极坐标方程为
．
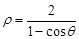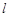与曲线C交于A、B两点，求
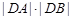的最小值．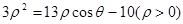
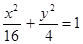，设P、Q分别为曲线C1与曲线C2上的任意一点，求|PQ|的最小值.
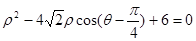，若点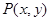
在该圆上，则
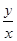的最大值是_______
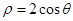的圆心到直线
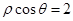的距离是__________.
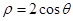，则该圆的圆心到直线
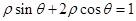的距离是______________________。
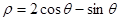，则该圆的半径为________．
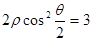化为直角坐标方程是 .