题目内容
已知函数f(x)=x2-x+13,|x-a|<1.
求证:|f(x)-f(a)|<2(|a|+1).
见解析
解析证明:|f(x)-f(a)|=|x2-x+13-(a2-a+13)|
=|x2-a2-x+a|=|(x-a)(x+a-1)|
=|x-a||x+a-1|<|x+a-1|=|x-a+2a-1|
≤|x-a|+|2a-1|<1+|2a|+1=2(|a|+1),
所以|f(x)-f(a)|<2(|a|+1).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 ,
,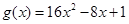 ,记
,记 的解集为M,
的解集为M, 的解集为N.
的解集为N. 时,证明:
时,证明: .
. ·an(n∈N+).
·an(n∈N+). ,求证:c1+c2+c3+…+cn<
,求证:c1+c2+c3+…+cn< .
.
 =x,求公园ABCD所占面积S关于x的函数解析式.
=x,求公园ABCD所占面积S关于x的函数解析式.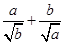 ≥
≥ +
+ .
.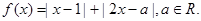 (1)当
(1)当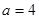 时,求不等式
时,求不等式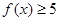 的解集;(2)若
的解集;(2)若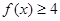 对
对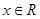 恒成立,求
恒成立,求 的取值范围.
的取值范围.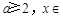 R.
R.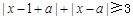 .
.