题目内容
用长度为24的材料围成一个矩形场地，中间有两道隔墙，要使矩形的面积最大，则隔墙的长度为分析：若设矩形场地的宽为x，则长为
，其面积为S=
•x，整理得x的二次函数，能求出函数的最值以及对应的x的值．
| 24-4x |
| 2 |
| 24-4x |
| 2 |
解答：解：如图所示，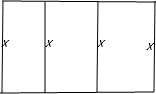
设矩形场地的宽为x，则长为
，其面积为：
S=
•x=12x-2x2=-2（x2-6x+9）+18=-2（x-3）2+18
当x=3时，S有最大值，为18；所以隔墙宽应为3．
故答案为：3．
设矩形场地的宽为x，则长为
| 24-4x |
| 2 |
S=
| 24-4x |
| 2 |
当x=3时，S有最大值，为18；所以隔墙宽应为3．
故答案为：3．
点评：本题借助于矩形的周长与面积，考查了二次函数的最值问题，是基础题目．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
用长度为24的材料围一矩形场地，中间加两道隔墙，要使矩形的面积最大，则隔墙的长度为（ ）
| A、3 | B、4 | C、6 | D、12 |