题目内容
10．已知函数f（x）=$\frac{1}{3}$x3-4x+4（x∈R），求f（x）的极大值与极小值．分析 f′（x）=x2-4，令f′（x）=0，解得x=±2，列出表格可得单调性与极值．
解答 解：f′（x）=x2-4，
令f′（x）=0，解得x=±2，
| x | （-∞，-2） | -2 | （-2，2） | 2 | （2，+∞） |
| f'（x） | + | 0 | - | 0 | + |
| f（x） | 递增 | 极大值 | 递减 | 极小值 | 递增 |
点评 本题考查了利用导数研究函数的单调性极值，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
15．若函数f（x）=x3+ax2+bx+a2在x=1时有极值10，则实数a，b的值是（ ）
| A． | $\left\{{\begin{array}{l}{a=-3}\\{b=3}\end{array}}\right.$ | B． | $\left\{{\begin{array}{l}{a=4}\\{b=-11}\end{array}}\right.$ | ||
| C． | $\left\{{\begin{array}{l}{a=-3}\\{b=3}\end{array}}\right.$或$\left\{{\begin{array}{l}{a=4}\\{b=-11}\end{array}}\right.$ | D． | $\left\{{\begin{array}{l}{a=-3}\\{b=-11}\end{array}}\right.$或$\left\{{\begin{array}{l}{a=4}\\{b=3}\end{array}}\right.$ |
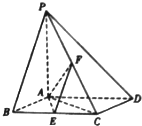如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，在四棱锥P-ABCD中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC=90°，PA=AB=BC=2，AD=1，M是棱PB中点．
如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的四个顶点所构成的菱形的边长是$\sqrt{5}$，面积是4，圆R：（x-4）2+y2=r2（6＞r＞2）与椭圆C交于点M与点N，连接RM并延长交椭圆于点P．