题目内容
变量x为区间[-2,1]上的一个随机数x、y为区间[-1,3]上的一个随机数.
(1)求y≤x的概率;
(2)求x2+y2-2y≤3的概率.
(1)求y≤x的概率;
(2)求x2+y2-2y≤3的概率.
(1)如图所示,
长方形ABCD的面积为S=3×4=12…(4分)
阴影部分的面积为S′=
=2…(6分)
所以y≤x的概率为
=
=
;…(7分)
(2)x2+y2-2y=3可以转化为圆的标准方程:x2+(y-1)2=4,该圆的圆心是(0,1),半径为2,…(9分)
在长方形ABCD与圆公共部分区域的面积为
×2+
=
+
,…(12分)
因此x2+y2-2y≤3的概率为
=
+
.…(13分)
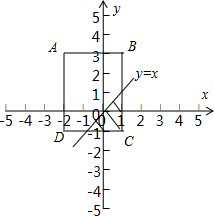
长方形ABCD的面积为S=3×4=12…(4分)
阴影部分的面积为S′=
| 2×2 |
| 2 |
所以y≤x的概率为
| S′ |
| S |
| 2 |
| 12 |
| 1 |
| 6 |
(2)x2+y2-2y=3可以转化为圆的标准方程:x2+(y-1)2=4,该圆的圆心是(0,1),半径为2,…(9分)
在长方形ABCD与圆公共部分区域的面积为
| 4π |
| 3 |
| 3 |
| 8π |
| 3 |
| 3 |
因此x2+y2-2y≤3的概率为
| ||||
| 12 |
| 2π |
| 9 |
| ||
| 12 |

练习册系列答案
相关题目
