题目内容
等差数列{an}中,a2=8,S6=66.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{cn}的通项为cn=2n,求数列{ancn}的前n项和An.
解:(Ⅰ)由a2=8,S6=66,得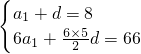 ,解得a1=6,d=2.∴数列{an}的通项公式an=2n+4.…(6分)
,解得a1=6,d=2.∴数列{an}的通项公式an=2n+4.…(6分)
(Ⅱ)由题意知ancn=(2n+4)•2n.…(8分)∴An=6•21+8•22+10•23+…+(2n+4)•2n,①
在上式两边同乘以2,得2An=6•22+8•23+10•24+…+(2n+4)•2n+1.②
①-②,得
-An=6•21+2•22+2•23+…+2•2n-(2n+4)•2n+1=4-(2n+2)•2n+1.
所以An=(n+1)2n+2-4.…(12分)
分析:(Ⅰ) 根据等差数列通项公式、前n项和公式建立a1,d的方程组,求出a1,d 后可得通项公式.
(Ⅱ)(Ⅱ)由题意知ancn=(2n+4)•2n 采用错位相消法求和即可.
点评:本题主要考查了等差数列通项公式、前n项和公式,方程思想,错位相消求和法.
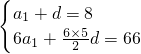 ,解得a1=6,d=2.∴数列{an}的通项公式an=2n+4.…(6分)
,解得a1=6,d=2.∴数列{an}的通项公式an=2n+4.…(6分)(Ⅱ)由题意知ancn=(2n+4)•2n.…(8分)∴An=6•21+8•22+10•23+…+(2n+4)•2n,①
在上式两边同乘以2,得2An=6•22+8•23+10•24+…+(2n+4)•2n+1.②
①-②,得
-An=6•21+2•22+2•23+…+2•2n-(2n+4)•2n+1=4-(2n+2)•2n+1.
所以An=(n+1)2n+2-4.…(12分)
分析:(Ⅰ) 根据等差数列通项公式、前n项和公式建立a1,d的方程组,求出a1,d 后可得通项公式.
(Ⅱ)(Ⅱ)由题意知ancn=(2n+4)•2n 采用错位相消法求和即可.
点评:本题主要考查了等差数列通项公式、前n项和公式,方程思想,错位相消求和法.

练习册系列答案
相关题目