题目内容
证明：如果函数y=f（x）在点x处可导，那么函数y=f（x）在点x处连续．
【答案】分析：要证明f（x）在点x处连续，就必须证明x→x时，f（x）的极限值为f（x），由f（x）在点x处可导，根据函数在点x处可导的定义，逐步进行两个转化，一个是趋向的转化，一个是形式（变成导数定义的形式）的转化．
解答：证明：设x=x+△x，则当x→x时，△x→0
则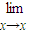
f（x）=
f（x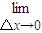+△x）=
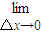[f（x+△x）-f（x）+f（x）]=
[
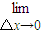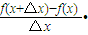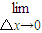
△x+f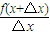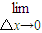（x）]
=
•
△x+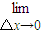
f（x）=f′（x）•0+f（x）=f（x）
∴函数f（x）在点x处连续．
点评：此题考查学生掌握函数连续的定义，灵活运用导数的定义．解题时要正确理解函数的连续性．
解答：证明：设x=x+△x，则当x→x时，△x→0
则
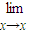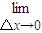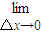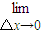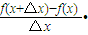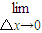
f（x）=f（x+△x）=[f（x+△x）-f（x）+f（x）]=[△x+f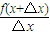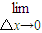（x）]=
•△x+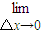f（x）=f′（x）•0+f（x）=f（x）∴函数f（x）在点x处连续．
点评：此题考查学生掌握函数连续的定义，灵活运用导数的定义．解题时要正确理解函数的连续性．
练习册系列答案
相关题目