题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() ,
,![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
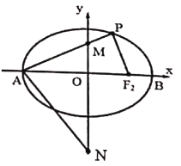
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴交于
轴交于![]() 点,过点
点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 轴与点
轴与点![]() ,试探究是否存在定点
,试探究是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过定点
为直径的圆恒过定点![]() .
.
【答案】(1)![]() ;(2)存在.
;(2)存在.
【解析】
(1)由当![]() 在
在![]() 轴时,
轴时,![]() 面积最大,得
面积最大,得![]() ,然后结合
,然后结合![]() 求解即可;
求解即可;
(2)先设![]() ,求出点
,求出点![]() ,
,![]() 的坐标,然后求出以
的坐标,然后求出以![]() 为直径的圆的方程,再结合
为直径的圆的方程,再结合![]() 在椭圆上,代入方程整理得圆的方程为
在椭圆上,代入方程整理得圆的方程为![]() ,然后令
,然后令![]() ,求解即可.
,求解即可.
解:(1)由题意知,当![]() 在
在![]() 轴时,
轴时,![]() 面积最大,
面积最大,
所以![]() ①,
①,
又![]() ②,
②,
联立①②,得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,其中
,其中![]() ,则
,则![]() ,
,![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即 ,
,
又![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即 ,
,
所以,以![]() 为直径的圆的方程为:
为直径的圆的方程为:
 ,
,
又 ,
,
且![]() 在椭圆上,
在椭圆上,
所以![]() ,
,
代入方程整理得圆的方程为
![]() ,
,
令![]() ,
,
则![]() ,
,
所以存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .
.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1

(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)
【题目】“难度系数”反映试题的难易程度,难度系数越大,题目得分率越高,难度也就越小.“难度系数”的计算公式为![]() ,其中,
,其中,![]() 为难度系数,
为难度系数,![]() 为样本平均失分,
为样本平均失分,![]() 为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度系数 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
测试后,随机抽取了50名学生的数据进行统计,结果如下:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
实测平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根据试卷2的难度系数估计这480名学生第2套试卷的平均分;
(2)从抽样的50名学生的5套试卷中随机抽取2套试卷,记这2套试卷中平均分超过96分的套数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试卷的预估难度系数和实测难度系数之间会有偏差.设![]() 为第
为第![]() 套试卷的实测难度系数,并定义统计量
套试卷的实测难度系数,并定义统计量![]() ,若
,若![]() ,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.


