题目内容
已知函数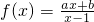 的图象经过
的图象经过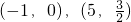 两点.
两点.
(1)求f(x)的解析式;
(2)求f(x)在区间[2,6]上的最大值与最小值.
(1)解:依题意得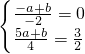
解得: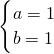
∴f(x)=
(2)任取2≤x1<x2≤6
∵f(x)=
∴f(x1)-f(x2)=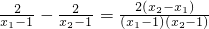
∵2≤x1<x2≤6
∴x2-x1>0,x1-1>0,x2-1>0,
从而f(x1)-f(x2)=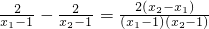 >0
>0
即f(x1)>f(x2),所以f(x)在[2,6]上为减函数,
从而f(x)max=f(2)=3,f(x)min=f(6)= .
.
分析:(1)根据函数f(x)的图象经过两点,建立关于a和b的方程组,解之即可;
(2)先根据函数单调性的定义判定出函数f(x)在区间[2,6]上的单调性,然后根据单调性将端点的函数值求出,即可求出最值.
点评:本题主要考查了函数的解析式的求解,以及分式函数的单调性的判定等有关知识,同时考查了分析问题的能力,属于基础题.
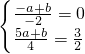
解得:
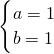
∴f(x)=

(2)任取2≤x1<x2≤6
∵f(x)=

∴f(x1)-f(x2)=
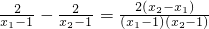
∵2≤x1<x2≤6
∴x2-x1>0,x1-1>0,x2-1>0,
从而f(x1)-f(x2)=
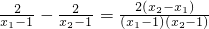 >0
>0即f(x1)>f(x2),所以f(x)在[2,6]上为减函数,
从而f(x)max=f(2)=3,f(x)min=f(6)=
 .
.分析:(1)根据函数f(x)的图象经过两点,建立关于a和b的方程组,解之即可;
(2)先根据函数单调性的定义判定出函数f(x)在区间[2,6]上的单调性,然后根据单调性将端点的函数值求出,即可求出最值.
点评:本题主要考查了函数的解析式的求解,以及分式函数的单调性的判定等有关知识,同时考查了分析问题的能力,属于基础题.

练习册系列答案
相关题目
 的图象经过点
的图象经过点 、
、 与点
与点 ,设函数
,设函数 在
在 和
和 处取到极值,其中
处取到极值,其中 ,
, 。
。 的二次项系数
的二次项系数 的值;
的值; 的大小(要求按从小到大排列);
的大小(要求按从小到大排列); ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 均相切,求
均相切,求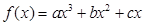 在点
在点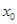 处取得极大值
处取得极大值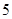 ,
,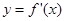 的图象经过点
的图象经过点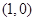 ,
,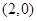 ,如图所示.
,如图所示.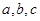 的值.
的值. 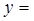

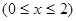 与
与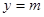 有两个不同的交点,
有两个不同的交点,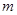 的取值范围。
的取值范围。