题目内容
在平面直角坐标系中,已知点A(1,0),向量e=(0,1),点B为直线x=-1上的动点,点C满足![]() ,点M满足
,点M满足![]() ,
,![]() .
.
(1)试求动点M的轨迹E的方程;
(2)试证直线CM为轨迹E的切线.
答案:
解析:
解析:
|
(1)解:设B( 由 设M(x,y),由 消去m得E的轨迹方程 (2)解:由题设知C为AB中点,MC⊥AB,故MC为AB的中垂线,MB∥x轴, 设M( 当y0≠0时, 将MC方程与 它有唯一解 又 当y0=0时,显然MC方程x=0为轨迹E的切线 综上知,MC为轨迹E的切线. |

练习册系列答案
相关题目
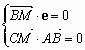 ,得
,得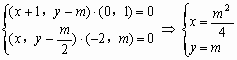 , 4分
, 4分