题目内容
．对于定义域和值域均为[0，1]的函数f（x），定义f1（x）=f（x），f2（x）=f（f1（x）），，…，fn（x）=f（fn-1（x）），n=1，2，3，…．满足fn（x）=x的点x∈[0，1]称为f的n阶周期点．设f（x）=
，则f的n阶周期点的个数是（ ）
A、2n B、2（2n-1） C、2n D、2n2
【答案】
C
【解析】
解：当x∈[0，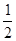
]时，f1（x）=2x=x，解得x=0
当x∈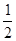（ ，1]时，f1（x）=2-2x=x，解得x=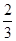
∴f的1阶周期点的个数是2
当x∈[0，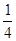
]时，f1（x）=2x，f2（x）=4x=x解得x=0
当x∈（ ，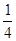
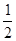]时，f1（x）=2x，f2（x）=2-4x=x解得x=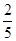
当x∈（ ，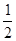
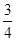]时，f1（x）=2-2x，f2（x）=-2+4x=x解得x=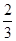
当x∈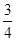（ ，1]时，f1（x）=2-2x，f2（x）=4-4x=x解得x=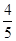 
∴f的2阶周期点的个数是22
依次类推
∴f的n阶周期点的个数是2n
故选C．
练习册系列答案
相关题目