题目内容
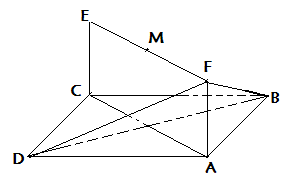
如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2, 是线段EF的中点.
是线段EF的中点.
(1)求证: ;(2)设二面角A—FD—B的大小为
;(2)设二面角A—FD—B的大小为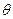 ,求
,求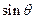 的值;
的值;
(3)设点P为一动点,若点P从M出发,沿棱按照 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
 是线段EF的中点.
是线段EF的中点.(1)求证:
 ;(2)设二面角A—FD—B的大小为
;(2)设二面角A—FD—B的大小为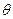 ,求
,求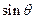 的值;
的值;(3)设点P为一动点,若点P从M出发,沿棱按照
 的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
的路线运动到点C,求这一过程中形成的三棱锥P—BFD的体积的最小值.
(1)易求得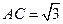 ,从而
,从而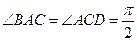 ,又
,又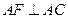 ,所以
,所以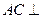 平面ABF,所以
平面ABF,所以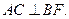 ………… 4分
………… 4分
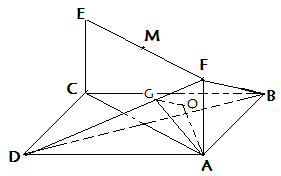
(2)易求得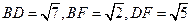 ,由勾股的逆定理知
,由勾股的逆定理知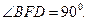 设点A在平面BFD内的射影为O,过A作
设点A在平面BFD内的射影为O,过A作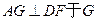 ,连结GO,则
,连结GO,则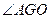 为二面角A—FD—B的平面角。即
为二面角A—FD—B的平面角。即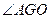
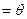 ,在
,在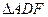 中,由等面积法易求得
中,由等面积法易求得 ,由等体积法求得点A到平面BFD的距离是
,由等体积法求得点A到平面BFD的距离是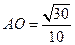 ,所以
,所以 ,即
,即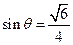
(3)设AC与BD相交于O,则OF//CM,所以CM//平面BFD。当点P在M或C时,三棱锥P—BFD的体积最小,
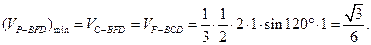
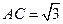 ,从而
,从而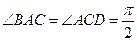 ,又
,又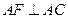 ,所以
,所以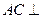 平面ABF,所以
平面ABF,所以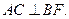 ………… 4分
………… 4分
(2)易求得
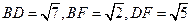 ,由勾股的逆定理知
,由勾股的逆定理知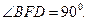 设点A在平面BFD内的射影为O,过A作
设点A在平面BFD内的射影为O,过A作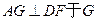 ,连结GO,则
,连结GO,则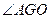 为二面角A—FD—B的平面角。即
为二面角A—FD—B的平面角。即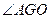
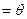 ,在
,在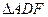 中,由等面积法易求得
中,由等面积法易求得 ,由等体积法求得点A到平面BFD的距离是
,由等体积法求得点A到平面BFD的距离是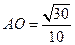 ,所以
,所以 ,即
,即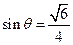
(3)设AC与BD相交于O,则OF//CM,所以CM//平面BFD。当点P在M或C时,三棱锥P—BFD的体积最小,
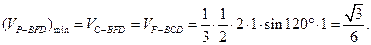
略

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 ,
,
 ,
, ,
,
 ,
,
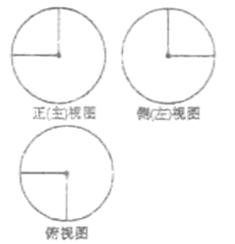
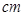 )如图3所示,则该几何体的侧面积为___________
)如图3所示,则该几何体的侧面积为___________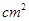 .
.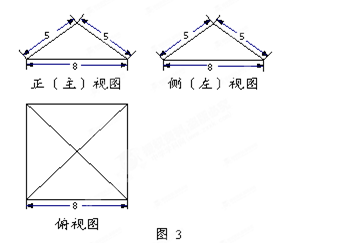








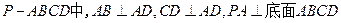 ,
,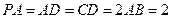 ,
,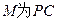 的中点.
的中点.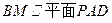 ;
;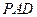 内找一点
内找一点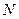 ,使
,使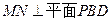 ,并求直线
,并求直线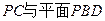 所成角的正弦值.
所成角的正弦值.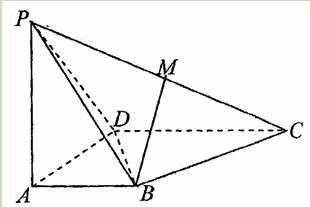
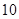 cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了
cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了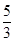 cm,则这个铁球的表面积为 ▲
cm,则这个铁球的表面积为 ▲ 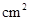 .
.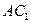 与平面
与平面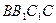 所成角的余弦值为
所成角的余弦值为