题目内容
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,圆
,圆![]() 过点
过点![]() ,且与
,且与![]() 交于
交于![]() ,
, ![]() 是等腰直角三角形,则圆
是等腰直角三角形,则圆![]() 的标准方程是____________
的标准方程是____________
【答案】![]()
【解析】
设A(﹣a,0),求得AF的中点B的坐标,可得圆F的半径和方程,设D(m,n),(m>0,n>0),E(m,﹣n),由△BDE为等腰直角三角形,可得m,n的关系,将D的坐标代入圆的方程,解方程可得m=1,求出n,代入椭圆方程,解方程可得a=2,即可得到圆F的方程.
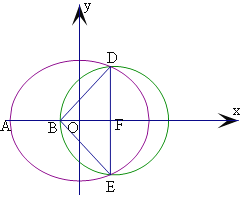
如图设A(﹣a,0),可得a>1,c=1,b2=a2﹣1,
线段AF的中点为B(![]() ,0),
,0),
圆F的圆心为F(1,0),半径r=|BF|![]() ,
,
设D(m,n),(m>0,n>0),E(m,﹣n),
由△BDE为等腰直角三角形,可得kBD=1,
即![]() 1,即n=m
1,即n=m![]() ,
,
由D在圆F:(x﹣1)2+y2=(![]() )2上,
)2上,
可得(m﹣1)2+(m![]() )2=(
)2=(![]() )2,
)2,
化简可得(m﹣1)(2m﹣1+a)=0,
解得m=1或m![]() (舍去),
(舍去),
则n![]() ,
,
将D(1,![]() )代入椭圆方程,可得
)代入椭圆方程,可得
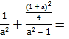 1,
1,
化简可得a=2或![]() (舍去),
(舍去),
则圆F的标准方程为(x﹣1)2+y2![]() ,
,
故答案为:(x﹣1)2+y2![]() .
.

练习册系列答案
相关题目