题目内容
 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,且AB=AD=1,
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,且AB=AD=1,BC=3,SB与平面ABCD所成的角为45°,E为SD的中点.
(Ⅰ)若F为线段BC上的一点且BF=
 BC,求证:EF∥平面SAB;
BC,求证:EF∥平面SAB;(Ⅱ)求点B到平面SDC的距离;
(Ⅲ)在线段 BC上是否存在一点G,使二面角G-SD-C的大小为arccos
 ?若存在,求出BG的长;若不存在,说明理由.
?若存在,求出BG的长;若不存在,说明理由.
【答案】分析:(Ⅰ)取SA的中点H,连接EH,BH,根据HE∥AD,BF∥AD,且HE= 可得四边形EFBH为平行四边形,则EF∥BH,BH?平面SAB,EF?平面SAB,根据线面平行的判定定理可知EF∥平面SAB.
可得四边形EFBH为平行四边形,则EF∥BH,BH?平面SAB,EF?平面SAB,根据线面平行的判定定理可知EF∥平面SAB.
(Ⅱ)求出面SDC的一个法向量,求点B到面SDC的距离实际上是求向量 在面SDC的法向量上的投影的长度.
在面SDC的法向量上的投影的长度.
(Ⅲ)假设存在点G(1,a,0)分别求出GSD面与面CSD的法向量,根据两法向量的夹角与二面角G-SD-C的大小相等或互补的关系,列出关于a的方程,有解且0<a<3则存在,否则不存在.
解答:解:(Ⅰ) 取SA的中点H,连接EH,BH.
由HE∥AD,BF∥AD,且HE=
∴HE∥BF,BF=HE,∴四边形EFBH为平行四边形.
∴EF∥BH,BH?平面SAB,EF?平面SAB,
∴EF∥平面SAB.

(Ⅱ)∵SA⊥底面ABCD∴∠SBA是AB与平面ABCD所成的角∴∠SBA=45°SA=AB=1
以A为原点,AB为x轴,图所示建立直角坐标系,

则B(1,0,0),S(0,0,1),D(0,1,0)C(1,3,0)
∴ =(1,2,0)
=(1,2,0) =(0.-1.1)
=(0.-1.1) =(0,3,0)
=(0,3,0)
设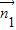 =(x1,y1,z1)是平SDC的法向量,则
=(x1,y1,z1)是平SDC的法向量,则 
∴ ∴
∴
取 B到平SDC的距离为d=
B到平SDC的距离为d= =
=
(Ⅲ) 假设存在,设BG=a,则G(1,a,0)(0<a<3)∴
设 =(x2,y2,z2)是平面DGS的法向量,则
=(x2,y2,z2)是平面DGS的法向量,则
∴ 取
取
由 =
= ,得a2=2+(1-a)2
,得a2=2+(1-a)2
∴ ,故线段 BC上存在一点G存在G点满足要求.且
,故线段 BC上存在一点G存在G点满足要求.且
点评:本题考直线和平面平行的判定,用向量法求点到平面的距离,二面角,考查学生计算能力,逻辑思维能力,方程思想,是中档题.
 可得四边形EFBH为平行四边形,则EF∥BH,BH?平面SAB,EF?平面SAB,根据线面平行的判定定理可知EF∥平面SAB.
可得四边形EFBH为平行四边形,则EF∥BH,BH?平面SAB,EF?平面SAB,根据线面平行的判定定理可知EF∥平面SAB.(Ⅱ)求出面SDC的一个法向量,求点B到面SDC的距离实际上是求向量
 在面SDC的法向量上的投影的长度.
在面SDC的法向量上的投影的长度.(Ⅲ)假设存在点G(1,a,0)分别求出GSD面与面CSD的法向量,根据两法向量的夹角与二面角G-SD-C的大小相等或互补的关系,列出关于a的方程,有解且0<a<3则存在,否则不存在.
解答:解:(Ⅰ) 取SA的中点H,连接EH,BH.
由HE∥AD,BF∥AD,且HE=

∴HE∥BF,BF=HE,∴四边形EFBH为平行四边形.
∴EF∥BH,BH?平面SAB,EF?平面SAB,
∴EF∥平面SAB.

(Ⅱ)∵SA⊥底面ABCD∴∠SBA是AB与平面ABCD所成的角∴∠SBA=45°SA=AB=1
以A为原点,AB为x轴,图所示建立直角坐标系,

则B(1,0,0),S(0,0,1),D(0,1,0)C(1,3,0)
∴
 =(1,2,0)
=(1,2,0) =(0.-1.1)
=(0.-1.1) =(0,3,0)
=(0,3,0)设
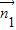 =(x1,y1,z1)是平SDC的法向量,则
=(x1,y1,z1)是平SDC的法向量,则 
∴
 ∴
∴
取
 B到平SDC的距离为d=
B到平SDC的距离为d= =
=
(Ⅲ) 假设存在,设BG=a,则G(1,a,0)(0<a<3)∴

设
 =(x2,y2,z2)是平面DGS的法向量,则
=(x2,y2,z2)是平面DGS的法向量,则
∴
 取
取
由
 =
= ,得a2=2+(1-a)2
,得a2=2+(1-a)2∴
 ,故线段 BC上存在一点G存在G点满足要求.且
,故线段 BC上存在一点G存在G点满足要求.且
点评:本题考直线和平面平行的判定,用向量法求点到平面的距离,二面角,考查学生计算能力,逻辑思维能力,方程思想,是中档题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,