Question

设不等式组

0≤x≤2 0≤y≤2

表示的平面区域为D．在区域D内随机取一个点，则此点到坐标原点的距离小于2的概率是（　　）

• A．

  π

  4

• B．

  π-2

  2

• C．

  π

  6

• D．

  4-π

  4

Answer 1

分析：根据题意，在区域D内随机取一个点P，则P点到坐标原点的距离小于2时，点P位于图中正方形OABC内，且在扇形OAC的内部，如图中的扇形部分．因此算出图中扇形部分面积，再除以正方形OABC面积，即得本题的概率．

解答：解：到坐标原点的距离小于2的点，位于以原点O为圆心、半径为2的圆内，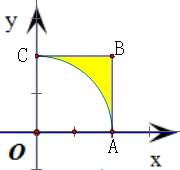
区域D：

0≤x≤2 0≤y≤2

表示正方形OABC，（如图）
其中O为坐标原点，A（2，0），B（2，2），C（0，2）．
因此在区域D内随机取一个点P，
则P点到坐标原点的距离大于2时，点P位于图中正方形OABC内，
且在扇形OAC的内部，如图中的扇形部分
∵S_{正方形OABC}=2²=4，S_扇形=

1

4

π•2²=π
∴所求概率为P=

S扇形

S正方形OABC

=

π

4

．
故选A．

点评：本题给出不等式组表示的平面区域，求在区域内投点使该到原点距离小于2的概率，着重考查了二元一次不等式组表示的平面区域和几何概型等知识点，属于基础题．