题目内容
20．使关于x的函数y=$\frac{ax+5}{2x-6}$的定义域与值域相同，则实数a=6．分析 可将原函数变成y=$\frac{1}{2}a+\frac{3a+5}{2x-6}$，从而可得出该函数的定义域及值域，而根据定义域和值域相同便可求出a．
解答 解：y=$\frac{\frac{1}{2}a（2x-6）+3a+5}{2x-6}=\frac{1}{2}a+\frac{3a+5}{2x-6}$；
∴该函数的定义域为{x|x≠3}，值域为{y|y$≠\frac{1}{2}a$}；
定义域和值域相同；
∴$\frac{1}{2}a=3$；
∴a=6．
故答案为：6．
点评 考查函数定义域、值域的定义，求定义域的方法：使原函数有意义，以及分离常数法求函数的值域．
练习册系列答案
相关题目
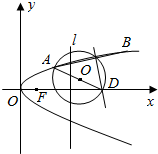如图，抛物线y2=2px（p＞0），F为抛物线的焦点，A，B是抛物线上互异的两点，直线AB与x轴不垂直，线段AB的中垂线交x轴于D（a，0），m=|$\overrightarrow{AF}$|+|$\overrightarrow{BF}$|．