题目内容
设m为实数,函数f(x)=2x2+(x-m)|x-m|,h(x)=
|
(1)若f(1)≥4,求m的取值范围;
(2)当m>0时,求证h(x)在[m,+∞)上是单调递增函数;
(3)若h(x)对于一切x∈[1,2],不等式h(x)≥1恒成立,求实数m的取值范围.
分析:(1)令x=1代入后对m的值进行讨论即可.
(2)先写出函数h(x)的解析式,然后用增函数的定义法证明.
(2)转化为二次函数,从而根据二次函数的单调性解出实数m的范围.
(2)先写出函数h(x)的解析式,然后用增函数的定义法证明.
(2)转化为二次函数,从而根据二次函数的单调性解出实数m的范围.
解答:解:(1)f(1)=2+(1-m)|1-m|≥4
当m>1时,(1-m)(m-1)≥2,无解;
当m≤1时,(1-m)(1-m)≥2,解得m≤1-
.
所以m≤1-
.
(2)由于m>0,x≥m.
所以h(x)=3x+
-2m.
任取m≤x1≤x2,h(x2)-h(x1)=(x2-x1)(
)
x2-x1>0,3x1x2-m2>3m2-m2>0,x1x2>0
所以h(x2)-h(x1)>0即:h(x)在[m,+∞)为单调递增函数.
(3)、①m<1时,x∈[1,2],f(x)=2x2+(x-m)(x-m)=3x2-2mx+m2,
h(x)=
≥1恒成立∴f(x)≥x恒成立,
即:g(x)=3x2-(2m+1)x+m2≥0
由于y=g(x)的对称轴为x=
<1
故g(x)在[1,2]为单调递增函数,
故g(1)≥0∴m2-2m+2≥0.
所以m<1.
②当1≤m≤2时,h(x)=
易证y=x-
+m在[1,m]为递增,
由②得y=3x+
-2m在[m,2]为递增,
所以,h(1)≥1,即0≤m≤2,
所以1≤m≤2.
③当m>2时,h(x)=x-
+2m(无解)
综上所述m≤2.
当m>1时,(1-m)(m-1)≥2,无解;
当m≤1时,(1-m)(1-m)≥2,解得m≤1-
| 2 |
所以m≤1-
| 2 |
(2)由于m>0,x≥m.
所以h(x)=3x+
| m2 |
| x |
任取m≤x1≤x2,h(x2)-h(x1)=(x2-x1)(
| 3x1x2-m2 |
| x1x2 |
x2-x1>0,3x1x2-m2>3m2-m2>0,x1x2>0
所以h(x2)-h(x1)>0即:h(x)在[m,+∞)为单调递增函数.
(3)、①m<1时,x∈[1,2],f(x)=2x2+(x-m)(x-m)=3x2-2mx+m2,
h(x)=
| f(x) |
| x |
即:g(x)=3x2-(2m+1)x+m2≥0
由于y=g(x)的对称轴为x=
| 2m+1 |
| 6 |
故g(x)在[1,2]为单调递增函数,
故g(1)≥0∴m2-2m+2≥0.
所以m<1.
②当1≤m≤2时,h(x)=
|
易证y=x-
| m2 |
| x |
由②得y=3x+
| m2 |
| x |
所以,h(1)≥1,即0≤m≤2,
所以1≤m≤2.
③当m>2时,h(x)=x-
| m2 |
| x |
综上所述m≤2.
点评:本题主要考查函数的单调性证明和应用.属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.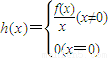 .
. .
. +2x+m,x∈R
+2x+m,x∈R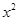 +2mx+1.
+2mx+1.