题目内容
设m为实数,函数f(x)=- +2x+m,x∈R
+2x+m,x∈R
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当m≤1且x>0时, >2
>2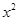 +2mx+1.
+2mx+1.
【答案】
(Ⅰ)增区间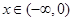 ,减区间
,减区间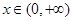 ;(Ⅱ)构造函数
;(Ⅱ)构造函数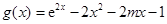 ,再证明
,再证明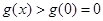 即可得证.
即可得证.
【解析】
试题分析:(Ⅰ)利用求导的方法求得单调区间,再求极值;(Ⅱ)先构造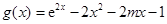 ,
,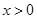 ,再证得
,再证得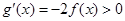 ,即
,即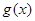 在
在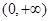 上为增函数,所以
上为增函数,所以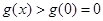 ,故
,故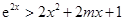 .
.
试题解析:(Ⅰ) ,令
,令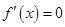 可得
可得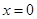 ,
,
易知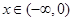 时
时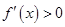 ,
,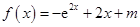 为增函数,
为增函数,
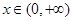 时
时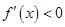 ,
,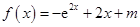 为减函数,
为减函数,
所以函数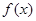 有极大值,无极小值,极大值为
有极大值,无极小值,极大值为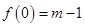 .
(6分)
.
(6分)
(Ⅱ)令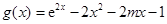 ,
,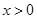 ,则
,则
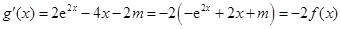 ,
,
由(Ⅰ)知,当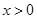 时,
时,
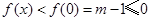 ,所以
,所以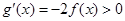 ,
,
故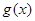 在
在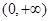 上为增函数,
上为增函数,
所以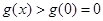 ,故
,故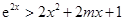 .
(12分)
.
(12分)
考点:1.用导数求函数的单调区间;2.利用导数的方法证明不等式.

练习册系列答案
相关题目
 .
. .
. .
.