题目内容
给出下列命题:①正切函数的图象的对称中心是唯一的;
②y=|sinx|、y=|tanx|的周期分别为π、
| π |
| 2 |
③若x1>x2,则sinx1>sinx2;
④若f(x)是R上的奇函数,它的最小正周期为T,则f(-
| T |
| 2 |
其中正确命题的序号是
分析:根据正切函数的性质判断①的正误,根据周期判断②的正误,正弦函数的性质判断③的正误,根据周期判断④的正误,推出结果即可.
解答:解:①正切函数的图象的对称中心是唯一的;有正切函数的性质可知,是错误的;
②y=|sinx|、y=|tanx|的周期分别为π、
;前者正确,后者错误,不正确;
③若x1>x2,则sinx1>sinx2;如果x1=390°,x2=90°,sinx1<sinx2;不正确;
④若f(x)是R上的奇函数,它的最小正周期为T,则f(-
)=0.f(x+π)=f(x),
f(-
+π)=f(
)=-f(-
)=-f(
),f(-
)=0正确.
故答案为:④
②y=|sinx|、y=|tanx|的周期分别为π、
| π |
| 2 |
③若x1>x2,则sinx1>sinx2;如果x1=390°,x2=90°,sinx1<sinx2;不正确;
④若f(x)是R上的奇函数,它的最小正周期为T,则f(-
| T |
| 2 |
f(-
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
| T |
| 2 |
故答案为:④
点评:本题考查正切函数的奇偶性与对称性,三角函数的周期性及其求法,正弦函数的单调性,正切函数的周期性,考查学生基本知识的灵活运用能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;
; )=0.
)=0.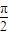 ;
;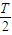 )=0.
)=0.