题目内容
(本小题满分14分)

如图,在三棱柱 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点.
(1)求证:AB⊥平面AA1 C1C;
(2)若线段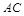 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 的位置,并说明理由;
的位置,并说明理由;
(3)证明: ⊥A1C.
⊥A1C.

如图,在三棱柱
 中,
中, 底面
底面 ,
, ,E、F分别是棱
,E、F分别是棱 的中点.
的中点.(1)求证:AB⊥平面AA1 C1C;
(2)若线段
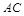 上的点
上的点 满足平面
满足平面 //平面
//平面 ,试确定点
,试确定点 的位置,并说明理由;
的位置,并说明理由;(3)证明:
 ⊥A1C.
⊥A1C.
(1)详见解析;(2) 是线段
是线段 的中点;(3)详见解析.
的中点;(3)详见解析.
 是线段
是线段 的中点;(3)详见解析.
的中点;(3)详见解析.试题分析:(1)求证:AB⊥平面AA1 C1C,证明线面垂直,只需证明线线垂直,即在平面
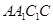 找两条直线与
找两条直线与 垂直,由已知
垂直,由已知 平面
平面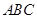 ,故
,故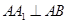 ,且
,且 ,故可证得结论;(2)线段
,故可证得结论;(2)线段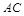 上的点
上的点 满足平面
满足平面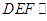 平面
平面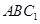 ,且面
,且面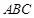
 面
面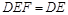 ,面
,面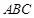
 面
面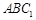
 ,由面面平行的性质可以得到
,由面面平行的性质可以得到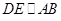 ,在
,在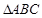 中,已知
中,已知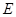 是
是 的中点,由中位线定理,即可确定点
的中点,由中位线定理,即可确定点 的位置;(3)证明:
的位置;(3)证明: ⊥A1C,证明线线垂直,只需证明一条直线垂直于另一条直线所在的平面,注意到四边形
⊥A1C,证明线线垂直,只需证明一条直线垂直于另一条直线所在的平面,注意到四边形 是一个正方形,则
是一个正方形,则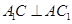 ,易证
,易证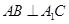 ,可得
,可得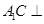 平面
平面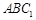 ,由(2)知平面
,由(2)知平面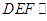 平面
平面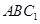 ,从而得
,从而得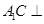 平面
平面 ,即可证得结论.
,即可证得结论.(1)
 底面
底面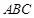 ,
,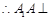
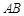 , 2分
, 2分 ,
,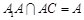 ,
,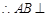 面
面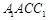 . 4分
. 4分(2)
 面
面 //面
//面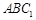 ,面
,面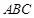
 面
面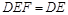 ,面
,面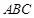
 面
面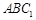
 ,
,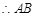 //
//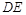 , 7分
, 7分 在
在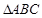 中
中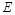 是棱
是棱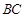 的中点,
的中点,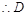 是线段
是线段 的中点. 8分
的中点. 8分(3)
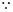 三棱柱
三棱柱 中
中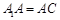
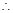 侧面
侧面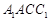 是菱形,
是菱形,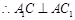 , 9分
, 9分由(1)可得
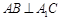 ,
,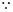
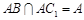 ,
,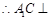 面
面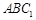 , 11分
, 11分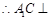
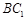 . 12分
. 12分又
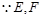 分别为棱
分别为棱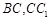 的中点,
的中点,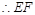 //
//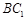 , 13分
, 13分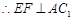 . 14分
. 14分
练习册系列答案
相关题目
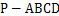 的底面
的底面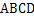 是平行四边形,
是平行四边形,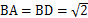 ,
,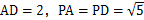 ,
,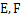 分别是棱
分别是棱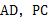 的中点.
的中点.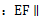 平面
平面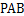 ;
;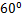 ,
,
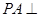 平面ABCD,AD//BC,
平面ABCD,AD//BC,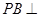 AC,
AC,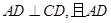
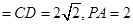 ,点M在线段PD上.
,点M在线段PD上.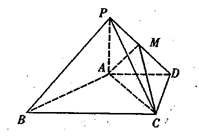
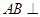 平面PAC;
平面PAC;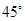 ,试确定点M的位置.
,试确定点M的位置.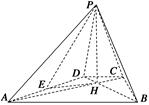

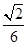 ,求线段AM的长.
,求线段AM的长.
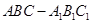 中,D、E分别是BC和
中,D、E分别是BC和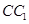 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.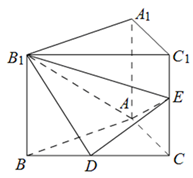
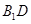 ⊥平面
⊥平面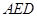 ;
;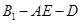 的余弦值;
的余弦值;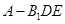 的体积.
的体积.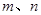 是不同的直线,
是不同的直线,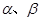 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: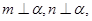 则
则
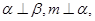 则
则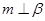
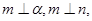 则
则
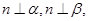 则
则

 平面PBC ②平面
平面PBC ②平面