题目内容
函数f(x)=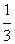 x3-mx2+(m2-4)x,x∈R。
x3-mx2+(m2-4)x,x∈R。
(1)当m=3时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)已知函数f(x)有三个互不相同的零点0,α ,β,且α<β。若对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,求实数m的取值范围。
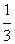 x3-mx2+(m2-4)x,x∈R。
x3-mx2+(m2-4)x,x∈R。(1)当m=3时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)已知函数f(x)有三个互不相同的零点0,α ,β,且α<β。若对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,求实数m的取值范围。
解:(1)当m=3时,f(x)=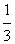 x3-3x2+5x,f ′(x)=x2-6x+5,
x3-3x2+5x,f ′(x)=x2-6x+5,
因为f(2)=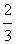 ,f ′(2)=-3,
,f ′(2)=-3,
所以切点坐标为(2,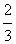 ),切线的斜率为-3.
),切线的斜率为-3.
则所求的切线方程为y-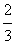 =-3(x-2),即9x+3y-20=0。
=-3(x-2),即9x+3y-20=0。
(2)f ′(x)=x2-2mx+(m2-4),
令f ′(x)=0,得x=m-2或x=m+2,
当x∈(-∞,m-2)时,f ′(x)>0,f(x)在(-∞,m-2)上是增函数;
当x∈(m-2,m+2)时,f ′(x)<0,f(x)在(m-2,m+2)上是减函数;
当x∈(m+2,+∞)时,f ′(x)>0,f(x)在(m+2,+∞)上是增函数;
因为函数f(x)有三个互不相同的零点0,α ,β,且f(x)=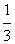 x[x2-3mx+3(m2-4)],
x[x2-3mx+3(m2-4)],
所以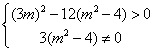 ,
,
解得:m∈(-4,-2)∪(-2,2)∪(2,4),
当m∈(-4,-2)时,m-2<m+2<0,所以α<m-2<β<m+2<0,
此时f(α)=0,f(1)>f(0)=0,与题意不合,故舍去;
当m∈(-2,2)时,m-2<0<m+2,所以α<m-2<0<m+2<β,
因为对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,所以α<1<β,
所以f(1)为函数f(x)在[α ,β]上的最小值;
因为当x=m+2时,函数f(x)在[α ,β]上取最小值,所以m+2=1,即m=-1;
当m∈(2,4)时,0<m-2<m+2,所以0<α<m-2<m+2<β,
因为对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,所以α<1<β,
所以f(1)为函数f(x)在[α ,β]上的最小值,
因为当x=m+2时,函数f(x)在[α ,β]上取最小值,所以m+2=1,即m=-1(舍去),
综上可知,m的取值范围是{-1}。
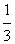 x3-3x2+5x,f ′(x)=x2-6x+5,
x3-3x2+5x,f ′(x)=x2-6x+5,因为f(2)=
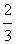 ,f ′(2)=-3,
,f ′(2)=-3,所以切点坐标为(2,
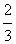 ),切线的斜率为-3.
),切线的斜率为-3.则所求的切线方程为y-
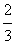 =-3(x-2),即9x+3y-20=0。
=-3(x-2),即9x+3y-20=0。(2)f ′(x)=x2-2mx+(m2-4),
令f ′(x)=0,得x=m-2或x=m+2,
当x∈(-∞,m-2)时,f ′(x)>0,f(x)在(-∞,m-2)上是增函数;
当x∈(m-2,m+2)时,f ′(x)<0,f(x)在(m-2,m+2)上是减函数;
当x∈(m+2,+∞)时,f ′(x)>0,f(x)在(m+2,+∞)上是增函数;
因为函数f(x)有三个互不相同的零点0,α ,β,且f(x)=
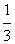 x[x2-3mx+3(m2-4)],
x[x2-3mx+3(m2-4)],所以
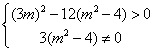 ,
,解得:m∈(-4,-2)∪(-2,2)∪(2,4),
当m∈(-4,-2)时,m-2<m+2<0,所以α<m-2<β<m+2<0,
此时f(α)=0,f(1)>f(0)=0,与题意不合,故舍去;
当m∈(-2,2)时,m-2<0<m+2,所以α<m-2<0<m+2<β,
因为对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,所以α<1<β,
所以f(1)为函数f(x)在[α ,β]上的最小值;
因为当x=m+2时,函数f(x)在[α ,β]上取最小值,所以m+2=1,即m=-1;
当m∈(2,4)时,0<m-2<m+2,所以0<α<m-2<m+2<β,
因为对任意的x∈[α ,β],都有f(x)≥f(1)恒成立,所以α<1<β,
所以f(1)为函数f(x)在[α ,β]上的最小值,
因为当x=m+2时,函数f(x)在[α ,β]上取最小值,所以m+2=1,即m=-1(舍去),
综上可知,m的取值范围是{-1}。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目