题目内容
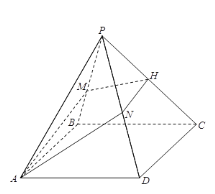
【题目】已知空间几何体![]() 中,
中,![]() 与
与![]() 均为边长为
均为边长为![]() 的等边三角形,
的等边三角形,![]() 为腰长为
为腰长为![]() 的等腰三角形,平面
的等腰三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
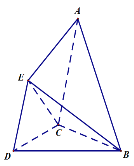
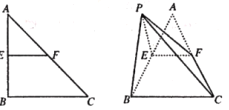
(1)试在平面![]() 内作一条直线,使直线上任意一点
内作一条直线,使直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明
平行,并给出详细证明
(2)求点![]() 到平面
到平面![]() 的距离
的距离
【答案】(1)见解析;(2)![]()
【解析】
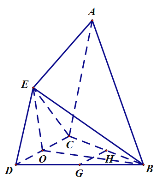
(1)取BC和BD的中点H、G,利用面面平行的判断定理证得平面CDE平行平面AHG即可求得结果;
(2)分别求得三角形ABC和CDE的面积以及求得E到平面ABC的距离,再利用等体积法![]() 即可求得
即可求得![]() 到平面
到平面![]() 的距离.
的距离.
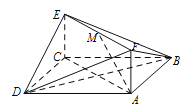
如图所示:取BC和BD的中点H、G,连接HG,HG为所求直线,
证明如下:因为BC和BD的中点H、G,所以![]() ,
,
又平面![]() 平面
平面![]() ,且
,且![]() 平面BCD
平面BCD
又平面![]() 平面
平面![]() .
.![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]()
所以![]() ,所以直线HG上任意一点
,所以直线HG上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行.
平行.
由(1)可得![]() ,即
,即![]() 平面ABC
平面ABC
所以点E到平面ABC的距离和点O到平面ABC的距离相等,记为![]()
三角形ABC的面积![]()
而三角形ACE的面积![]()
用等体积法![]() 可得:
可得:
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: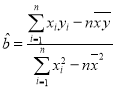 ,
,![]() ,
,![]() ,
,![]() .
.