题目内容
设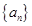 是公差不为零的等差数列,
是公差不为零的等差数列,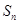 为其前
为其前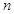 项和,满足
项和,满足 且
且 、
、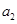 、
、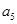 成等比数列.
成等比数列.
(Ⅰ)求数列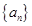 的通项公式;
的通项公式;
(Ⅱ)设数列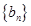 满足:
满足: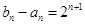 ,
,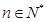 ,
, 为数列
为数列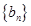 的前
的前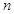 项和,问是否存在正整数
项和,问是否存在正整数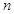 ,使得
,使得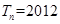 成立?若存在,求出
成立?若存在,求出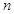 ;若不存在,请说明理由.
;若不存在,请说明理由.
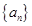 是公差不为零的等差数列,
是公差不为零的等差数列,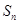 为其前
为其前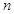 项和,满足
项和,满足 且
且 、
、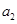 、
、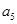 成等比数列.
成等比数列.(Ⅰ)求数列
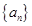 的通项公式;
的通项公式;(Ⅱ)设数列
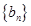 满足:
满足: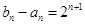 ,
,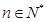 ,
, 为数列
为数列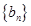 的前
的前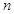 项和,问是否存在正整数
项和,问是否存在正整数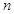 ,使得
,使得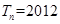 成立?若存在,求出
成立?若存在,求出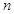 ;若不存在,请说明理由.
;若不存在,请说明理由.(Ⅰ)  (Ⅱ)不存在正整数
(Ⅱ)不存在正整数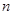 ,使得
,使得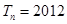 成立。
成立。
 (Ⅱ)不存在正整数
(Ⅱ)不存在正整数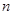 ,使得
,使得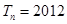 成立。
成立。本题主要考查等比数列的定义和性质,等差数列的通项公式、前n项和公式的应用,求出an=2n,是解题的关键,属于中档题.
(Ⅰ)由a1,a2,a4 成等比数列得:(a1+2)2=a1(a1+6),解得a1=2,即可得到数列{an}的通项公式an的解析式.
(Ⅱ)由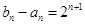 ,可得b1•b2•…•bn =41+2+…+n,利用等差数列的前n项和公式运算求得最后结果.
,可得b1•b2•…•bn =41+2+…+n,利用等差数列的前n项和公式运算求得最后结果.
解:(I)设数列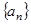 的公差为
的公差为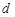 ,且
,且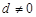
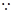
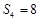 且
且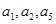 成等比数列.
成等比数列.
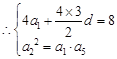 ,即
,即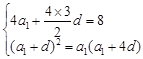
解得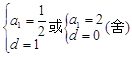 ……3分
……3分
∴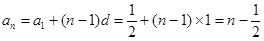 ……6分
……6分
(II)由题知: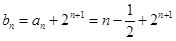 ,
,
∴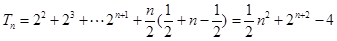 u…………10分
u…………10分
若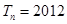 ,则
,则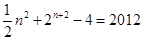 ,即
,即
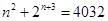
令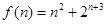 ,知
,知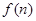 单调递增,
单调递增,
当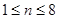 时,
时,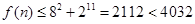
当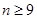 时,
时,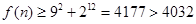 ,
,
故不存在正整数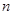 ,使得
,使得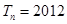 成立。 …………14分
成立。 …………14分
(Ⅰ)由a1,a2,a4 成等比数列得:(a1+2)2=a1(a1+6),解得a1=2,即可得到数列{an}的通项公式an的解析式.
(Ⅱ)由
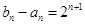 ,可得b1•b2•…•bn =41+2+…+n,利用等差数列的前n项和公式运算求得最后结果.
,可得b1•b2•…•bn =41+2+…+n,利用等差数列的前n项和公式运算求得最后结果.解:(I)设数列
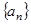 的公差为
的公差为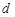 ,且
,且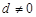
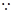
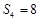 且
且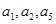 成等比数列.
成等比数列.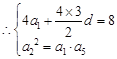 ,即
,即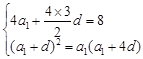
解得
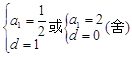 ……3分
……3分 ∴
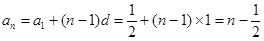 ……6分
……6分(II)由题知:
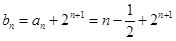 ,
,∴
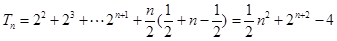 u…………10分
u…………10分若
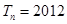 ,则
,则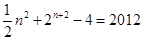 ,即
,即
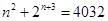
令
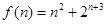 ,知
,知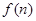 单调递增,
单调递增, 当
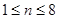 时,
时,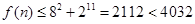
当
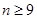 时,
时,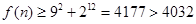 ,
,故不存在正整数
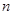 ,使得
,使得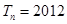 成立。 …………14分
成立。 …………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
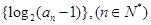 为等差数列,且
为等差数列,且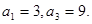 求
求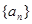 的通项式;
的通项式;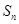 。
。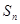 ﹥0成立的最大自然数n的值为.
﹥0成立的最大自然数n的值为. 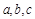 成等差数列,
成等差数列,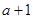 ,
,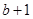 ,
,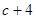 成等比数列,
成等比数列,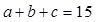 ,求
,求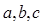 .
.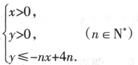 表示的平面区域为
表示的平面区域为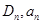 表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则
表示区域Dn中整点的个数(其中整点是指横、纵坐标都是整数的点),则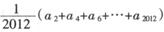 =( )
=( )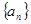 的前
的前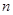 项和为
项和为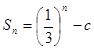 ,正数数列
,正数数列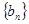 的首项为
的首项为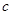 ,
,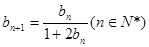 .记数列
.记数列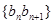 前
前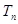 .
.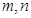 ,且
,且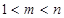 ,使得
,使得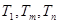 成等比数列?若存在,求出
成等比数列?若存在,求出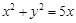 内,过点
内,过点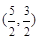 有
有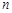 条弦的长度成等差数列,最短弦长为数列的首项
条弦的长度成等差数列,最短弦长为数列的首项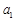 ,最长弦为
,最长弦为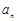 ,若公差
,若公差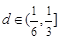 ,则
,则 .
.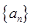 的前n项和为
的前n项和为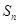 ,已知
,已知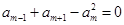 ,
,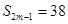 ,则
,则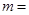 ( )
( )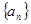 的各项均为正数,
的各项均为正数,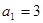 ,前三项的和为21,则
,前三项的和为21,则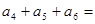 __________.
__________.