题目内容
 (2013•广州三模)如图所示,圆柱的高为2,底面半径为
(2013•广州三模)如图所示,圆柱的高为2,底面半径为| 3 |
(1)求证:平面AEB∥平面DFC;
(2)求证:BC⊥BE;
(3)求四棱锥E-ABCD体积的最大值.
分析:(1)根据圆柱的上下底面平行,利用面面平行与线面平行的性质证出AD∥BC,结合AD=BC得四边形ABCD是平行四边形,从而AB∥CD,由线面平行的判定证出AB∥平面DFC,同理得出AE∥平面DFC,最后根据面面平行判定定理,即可得到平面AEB∥平面DFC;
(2)由(1)得四边形BCFE为平行四边形,结合圆内接四边形的性质,得到四边形BCFE为矩形,得到BC⊥BE,而AE⊥平面BCFE,得AE⊥BC,根据线面垂直的判定定理得BC⊥平面ABE,从而证出BC⊥BE;
(3)由锥体的体积公式,得VE-ABCD=2VE-ABC=2VA-BCE,而VA-BCE=
S△BCE×AE=
S△BCE,在底面圆中研究内接△BCE的面积,可得当且仅当BE=BC=
时面积有最大值,由此即可算出四棱锥E-ABCD体积的最大值.
(2)由(1)得四边形BCFE为平行四边形,结合圆内接四边形的性质,得到四边形BCFE为矩形,得到BC⊥BE,而AE⊥平面BCFE,得AE⊥BC,根据线面垂直的判定定理得BC⊥平面ABE,从而证出BC⊥BE;
(3)由锥体的体积公式,得VE-ABCD=2VE-ABC=2VA-BCE,而VA-BCE=
| 1 |
| 3 |
| 2 |
| 3 |
| 6 |
解答:解:(1)由圆柱的性质,可得:AD∥平面BCFE
又∵过AD作圆柱的截面交下底面于BC.∴AD∥BC,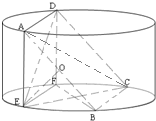
∵AD=BC,可得四边形ABCD是平行四边形,∴AB∥CD
∵AB?平面DFC,CD?平面DFC,∴AB∥平面DFC,
由平行四边形ADFE中AE∥DF,同理可得AE∥平面DFC,
∵AE、AB是平面AEB内的相交直线,∴平面AEB∥平面DFC;
(2)由(1)得BC
EF,∴四边形BCFE为平行四边形
又∵四边形BCFE是圆内接四边形,∴四边形BCFE为矩形,可得BC⊥BE,
又∵圆柱的母线AE⊥平面BCFE,BC?平面BCFE,∴AE⊥BC,
∵BE、AE是平面ABE内两条相交直线,∴BC⊥平面ABE
结合BE?平面ABE,可得BC⊥BE;
(3)由锥体的体积公式,可得
四棱锥E-ABCD体积VE-ABCD=2VE-ABC=2VA-BCE,
∵AE⊥平面BCFE,∴AE=2为三棱锥A-BCE的高,
可得VA-BCE=
S△BCE×AE=
S△BCE
∵底面半径r=
,四边形BCFE为矩形
∴S△BCE=
SBCFE≤r2=3,可得VA-BCE≤
×3=2
因此四棱锥E-ABCD体积VE-ABCD=2VA-BCE≤4,当且仅当BE=BC=
时等号成立
∴四棱锥E-ABCD体积的最大值为4.
又∵过AD作圆柱的截面交下底面于BC.∴AD∥BC,

∵AD=BC,可得四边形ABCD是平行四边形,∴AB∥CD
∵AB?平面DFC,CD?平面DFC,∴AB∥平面DFC,
由平行四边形ADFE中AE∥DF,同理可得AE∥平面DFC,
∵AE、AB是平面AEB内的相交直线,∴平面AEB∥平面DFC;
(2)由(1)得BC
| ∥ |
. |
又∵四边形BCFE是圆内接四边形,∴四边形BCFE为矩形,可得BC⊥BE,
又∵圆柱的母线AE⊥平面BCFE,BC?平面BCFE,∴AE⊥BC,
∵BE、AE是平面ABE内两条相交直线,∴BC⊥平面ABE
结合BE?平面ABE,可得BC⊥BE;
(3)由锥体的体积公式,可得
四棱锥E-ABCD体积VE-ABCD=2VE-ABC=2VA-BCE,
∵AE⊥平面BCFE,∴AE=2为三棱锥A-BCE的高,
可得VA-BCE=
| 1 |
| 3 |
| 2 |
| 3 |
∵底面半径r=
| 3 |
∴S△BCE=
| 1 |
| 2 |
| 2 |
| 3 |
因此四棱锥E-ABCD体积VE-ABCD=2VA-BCE≤4,当且仅当BE=BC=
| 6 |
∴四棱锥E-ABCD体积的最大值为4.
点评:本题着重考查了线面平行的判定定理、面面平行的判定与性质、线面垂直的判定与性质、锥体的体积公式及其推论和圆内接三角形面积的最值求法等知识,属于中档题.

练习册系列答案
相关题目
 (2013•广州三模)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,PA=AD=AB=2BC,M,N分别为PC,PB的中点.
(2013•广州三模)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,PA=AD=AB=2BC,M,N分别为PC,PB的中点. (2013•广州三模)如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上一点,且
(2013•广州三模)如图,长为m+1(m>0)的线段AB的两个端点A和B分别在x轴和y轴上滑动,点M是线段AB上一点,且 (2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=
(2013•广州三模)如图,在等腰梯形PDCB中,PB∥CD,PB=3,DC=1,PD=BC=