Question

（2013•广州三模）如图，在四棱锥P-ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，PA=AD=AB=2BC，M，N分别为PC，PB的中点．
（Ⅰ）求证：PB⊥DM；
（Ⅱ）求CD与平面ADMN所成的角的正弦值．

Answer 1

分析：（Ⅰ）解法1 先由AD⊥PA．AD⊥AB，证出AD⊥平面PAB得出AD⊥PB．又N是PB的中点，PA=AB，得出AN⊥PB．证出PB⊥平面ADMN后，即可证出PB⊥DM．
 解法2：如图，以A为坐标原点建立空间直角坐标系A-xyz，设BC=1，通过证明

PB

•

DM

=0证出PB⊥DM 
 （Ⅱ）解法1：取AD中点Q，连接BQ和NQ，则BQ∥DC，又PB⊥平面ADMN，所以CD与平面ADMN所成的角为∠BQN．在Rt△BQN中求解即可．
 解法2，通过 PB⊥平面ADMN，可知

PB

 是平面ADMN 的一个法向量，?

PB

，

DC

＞的余角即是CD与平面ADMN所成的角．

解答：（本题满分13分）
解：（Ⅰ）解法1：∵N是PB的中点，PA=AB，∴AN⊥PB．
∵PA⊥平面ABCD，所以AD⊥PA．
又AD⊥AB，PA∩AB=A，∴AD⊥平面PAB，AD⊥PB．
又AD∩AN=A，∴PB⊥平面ADMN．
∵DM?平面ADMN，∴PB⊥DM．                   …（6分）
解法2：如图，以A为坐标原点建立空间直角坐标系A-xyz，设BC=1，
可得，A（0，0，0），P（0，0，2），B（2，0，0），C（2，1，0），M(1，

1

2

，1)，D（0，2，0）．
因为 

PB

•

DM

=(2，0，-2)•(1，-

3

2

，1)=0，所以PB⊥DM．  …（6分）

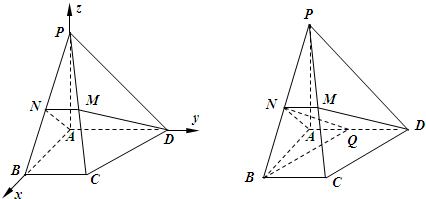
（Ⅱ）解法1：取AD中点Q，连接BQ和NQ，则BQ∥DC，又PB⊥平面ADMN，∴CD与平面ADMN所成的角为∠BQN．
设BC=1，在Rt△BQN中，则BN=

2

，BQ=

5

，故sin∠BQN=

10

5

．
所以CD与平面ADMN所成的角的正弦值为

10

5

．          …（13分）
解法2：因为

PB

•

AD

=(2，0，-2)•(0，2，0)=0．
所以 PB⊥AD，又PB⊥DM，所以PB⊥平面ADMN，
因此?

PB

，

DC

＞的余角即是CD与平面ADMN所成的角．
因为 cos?

PB

，

DC

＞=

PB • DC

| PB || DC |

=

10

5

．
所以CD与平面ADMN所成的角的正弦值为

10

5

．         …（13分）

点评：本题主要考查空间角，距离的计算，线面垂直，面面垂直的定义，性质、判定，考查了空间想象能力、计算能力，分析解决问题能力．空间问题平面化是解决空间几何体问题最主要的思想方法．