题目内容
【题目】函数![]() 的部分图像如图所示.
的部分图像如图所示.

(1)求函数![]() 的解析式;
的解析式;
(2)求图中![]() 的值及函数
的值及函数![]() 的单调递减区间;
的单调递减区间;
(3)若将![]() 的图象向左平移
的图象向左平移![]() 个单位后,得到
个单位后,得到![]() 的图像关于直线
的图像关于直线![]() 对称,求
对称,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,递减区间为
,递减区间为![]() ,
,![]() ;(3)
;(3)![]()
【解析】
(1)通过图象直接可求出![]() ,通过图象可以知道函数的零点的坐标,这样可以求出函数的周期,利用周期公式,可以求出
,通过图象可以知道函数的零点的坐标,这样可以求出函数的周期,利用周期公式,可以求出![]() 的值,把其中一个零点的坐标代入解析式中,结合已知可以求出
的值,把其中一个零点的坐标代入解析式中,结合已知可以求出![]() 值;
值;
(2)令![]() 和利用周期性,分别可以
和利用周期性,分别可以![]() 的值,再根据正弦型函数的单调性,写出函数的单调递减区间;
的值,再根据正弦型函数的单调性,写出函数的单调递减区间;
(3)根据平移的过程,写出平移后的函数解析式,把![]() 代入平移后的解析式中,使得新函数达到最值点,这样结合已知可以求出
代入平移后的解析式中,使得新函数达到最值点,这样结合已知可以求出![]() 的最小值.
的最小值.
(1)由题可知,![]() ,
,![]() ,
,![]() ,
,![]() .
.
将点![]() 代入
代入![]() 得
得![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
(2)由题可知:![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,![]() ,
,
故函数![]() 的递减区间为
的递减区间为![]() ,
,![]() .
.
(3)![]() ,
,![]() ,
,
![]() ,
,![]() ,又
,又![]() ,
,![]() .
.

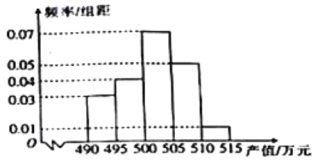
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了![]() 月
月![]() 日至
日至![]() 月
月![]() 日的每天昼夜温差与实验室每天每
日的每天昼夜温差与实验室每天每![]() 颗种子中的发芽数,得到如下资料:
颗种子中的发芽数,得到如下资料:
日期 |
|
|
|
|
|
温差 |
|
|
|
|
|
发芽数 |
|
|
|
|
|
该农科所确定的研究方案是:先从这![]() 组数据中选取
组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再对被选取的
组数据求线性回归方程,再对被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是不相邻两天数据的概率;
组数据恰好是不相邻两天数据的概率;
(2)若选取的是![]() 月
月![]() 日与
日与![]() 月
月![]() 日的数据,请根据
日的数据,请根据![]() 月
月![]() 日至
日至![]() 月
月![]() 日的数据求出
日的数据求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?
颗.则认为得到的线性回归方程是可靠的.试问(2)中所得到的线性回归方程是可靠的吗?
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,![]() .
.
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|