题目内容
设关于 的函数
的函数 的最小值为
的最小值为 ,试确定满足
,试确定满足 的
的 的值,并对此时的
的值,并对此时的 值求
值求 的最大值。
的最大值。
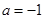 ,此时
,此时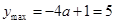 。
。
解析试题分析:解:令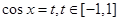 ,则
,则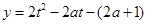 ,对称轴
,对称轴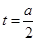 ,
,
当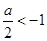 ,即
,即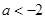 时,
时,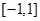 是函数
是函数 的递增区间,
的递增区间,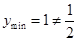 ;
;
当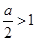 ,即
,即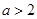 时,
时,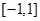 是函数
是函数 的递减区间,
的递减区间,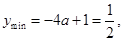
得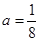 ,与
,与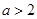 矛盾;
矛盾;
当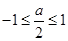 ,即
,即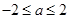 时,
时,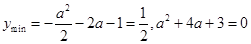
得 或
或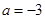 ,
,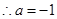 ,此时
,此时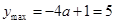 。
。
考点:三角函数的性质
点评:主要是考查了三角函数的性质的运用以及分类讨论思想的运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
设关于 的函数
的函数 的最小值为
的最小值为 ,试确定满足
,试确定满足 的
的 的值,并对此时的
的值,并对此时的 值求
值求 的最大值。
的最大值。
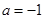 ,此时
,此时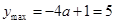 。
。
解析试题分析:解:令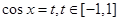 ,则
,则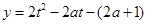 ,对称轴
,对称轴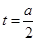 ,
,
当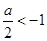 ,即
,即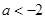 时,
时,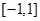 是函数
是函数 的递增区间,
的递增区间,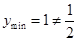 ;
;
当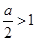 ,即
,即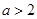 时,
时,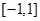 是函数
是函数 的递减区间,
的递减区间,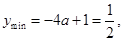
得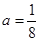 ,与
,与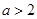 矛盾;
矛盾;
当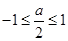 ,即
,即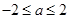 时,
时,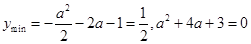
得 或
或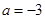 ,
,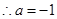 ,此时
,此时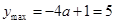 。
。
考点:三角函数的性质
点评:主要是考查了三角函数的性质的运用以及分类讨论思想的运用,属于中档题。

 名校课堂系列答案
名校课堂系列答案