题目内容
(12分)证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得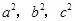 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△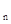 ,其边长
,其边长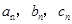 为正整数且
为正整数且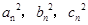 成等差数列。
成等差数列。
【答案】
解:(Ⅰ)考虑到结构要证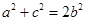 ,;类似勾股数进行拼凑。
,;类似勾股数进行拼凑。
证明:考虑到结构特征,取特值 满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
满足等差数列,只需取b=5a,c=7a,对一切正整数a均能成立。
结合第一问的特征,将等差数列分解,通过一个可做多种结构分解的因式说明构成三角形,再证明互不相似,且无穷。
证明:当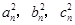 成等差数列,则
成等差数列,则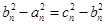 ,
,
分解得: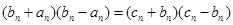
选取关于n的一个多项式,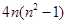 做两种途径的分解
做两种途径的分解
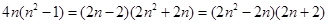
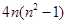
对比目标式,构造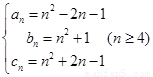 ,由第一问结论得,等差数列成立,
,由第一问结论得,等差数列成立,
考察三角形边长关系,可构成三角形的三边。
下证互不相似。
任取正整数m,n,若△m,△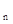 相似:则三边对应成比例
相似:则三边对应成比例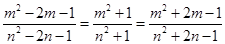 ,
,
由比例的性质得: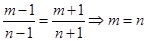 ,与约定不同的值矛盾,故互不相似。
,与约定不同的值矛盾,故互不相似。
【解析】略

练习册系列答案
相关题目
 ,都存在正整数
,都存在正整数 ,使得
,使得 成等差数列;
成等差数列; ,其边长
,其边长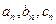 为正整数且
为正整数且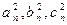 成等差数列.
成等差数列.  成等差数列。
成等差数列。 ,其边长
,其边长 为正整数且
为正整数且 成等差数列。
成等差数列。